
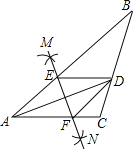
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,求线段BE的长.

【答案】8.
【解析】
试题分析:根据作法得到MN是线段AD的垂直平分线,则AE=DE,AF=DF,所以∠EAD=∠EDA,加上∠BAD=∠CAD,得到∠EDA=∠CAD,则可判断DE∥AC,同理DF∥AE,于是可判断四边形AEDF是平行四边形,加上EA=ED,则可判断四边形AEDF为菱形,所以AE=DE=DF=AF=4,然后利用平行线分线段成比例可计算BE的长.
解:根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是平行四边形,
而EA=ED,
∴四边形AEDF为菱形,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴BE:AE=BD:CD,即BE:4=6:3,
∴BE=8.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】海水受日月的引力而产生潮汐现象.早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.某港口某天从0时到12时的水深情况如下表,其中T表示时刻,h表示水深.
T(时) | 0 | 3 | 6 | 9 | 12 |
h(米) | 5 | 7.4 | 5.1 | 2.6 | 4.5 |
上述问题中,字母T,h表示的是变量还是常量,简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
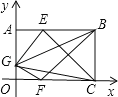
【题目】如图,已知OABC是一个长方形,其中顶点A,B的坐标分别为(0,a)和(9,a),点E在AB上,且AE=AG,点F在OC上,且OF=![]() OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.
OC,点G在OA上,且使△GEC的面积为20,△GFB的面积为16,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿。其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。凡百钱买鸡百只,问鸡翁、母、雏各几何。”

译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱。现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?
结合你学过的知识,解决下列问题:
(1)若设公鸡有x只,母鸡有y只,
①则小鸡有____________只,买小鸡一共花费____________文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程: ______________________________;
(2)若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?
(3)除了问题(2)中的解之外,请你再直接写出两组符合“百鸡问题”的解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②a+b+c>0;③c=﹣3a;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
其中正确的结论是 .(只填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com