
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOAЃН2ЃЌOCЃН3ЃЎ
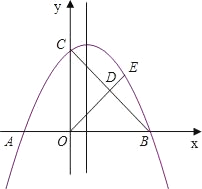
гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOAЃН2ЃЌOCЃН3ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉзїRtЁїOBCЕФИпODЃЌбгГЄODгыХзЮяЯпдкЕквЛЯѓЯоФкНЛгкЕуEЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉЂйдкxжсЩЯЗНЕФХзЮяЯпЩЯЃЌЪЧЗёДцдквЛЕуPЃЌЪЙЫФБпаЮOBEPЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂкдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЪЧЗёДцдкЩЯЕуQЃЌЪЙЕУЁїBEQЕФжмГЄзюаЁЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+
x2+![]() x+3ЃЛЃЈ2ЃЉЃЈ2ЃЌ2ЃЉЃЛЃЈ3ЃЉЂйДцдкЃЌЃЈЉ1ЃЌ2ЃЉЃЛЂкДцдкЃЌЃЈ
x+3ЃЛЃЈ2ЃЉЃЈ2ЃЌ2ЃЉЃЛЃЈ3ЃЉЂйДцдкЃЌЃЈЉ1ЃЌ2ЃЉЃЛЂкДцдкЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвбжЊЬѕМўЕУГіAЕуМАCЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉyЃН0ДњШыЃЈ1ЃЉжаЫљЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМДПЩЕФГіДЫКЏЪ§гыxжсЕФНЛЕузјБъЃЌгЩODЦНЗжЁЯBOCПЩжЊOEЫљдкЕФжБЯпЮЊyЃНxЃЌдйНтДЫжБЯпгыХзЮяЯпзщГЩЕФЗНГЬзщМДПЩЧѓГіEЕузјБъЃЛ
ЃЈ3ЃЉЂйЙ§ЕуEзїxжсЕФЦНааЯпгыХзЮяЯпНЛгкСэвЛЕуPЃЌСЌНгBEЁЂPOЃЌАбyЃН2ДњШыЖўДЮКЏЪ§НтЮіЪНМДПЩЧѓГіPЕузјБъЃЌНјЖјПЩЕУГіЫФБпаЮOBEPЪЧЦНааЫФБпаЮЃЛ
ЂкЩшQЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌСЌНгQAЁЂQBЁЂQEЁЂBEЃЌгЩQAЃНQBПЩжЊЁїBEQЕФжмГЄЕШгкBE+QA+QEЃЌгЩAЁЂEСНЕуЕФзјБъПЩЕУГіжБЯпAEЕФНтЮіЪНЃЌдйИљОнХзЮяЯпЕФЖдГЦжсЪЧxЃН![]() ПЩЧѓГіQЕуЕФзјБъЃЌНјЖјПЩЕУГіНсТлЃЎ
ПЩЧѓГіQЕуЕФзјБъЃЌНјЖјПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЁпOAЃН2ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЎ
ЁпOCЃН3ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ЁпАбЃЈЉ2ЃЌ0ЃЉЃЌЃЈ0ЃЌ3ЃЉДњШыyЃНЉ![]() x2+bx+cЃЌЕУ
x2+bx+cЃЌЕУ![]() НтЕУ
НтЕУ![]()
ЁрХзЮяЯпНтЮіЪНЮЊyЃНЉ![]() x2+
x2+![]() x+3ЃЛ
x+3ЃЛ
ЃЈ2ЃЉАбyЃН0ДњШыyЃНЉ![]() x2+
x2+![]() x+3ЃЌ
x+3ЃЌ
НтЕУx1ЃНЉ2ЃЌx2ЃН3
ЁрЕуBЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЌ
ЁрOBЃНOCЃН3
ЁпODЁЭBCЃЌ
ЁрODЦНЗжЁЯBOC
ЁрOEЫљдкЕФжБЯпЮЊyЃНx
НтЗНГЬзщ ЕУ
ЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпЕуEдкЕквЛЯѓЯоФкЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ2ЃЌ2ЃЉЃЎ
ЃЈ3ЃЉЂйДцдкЃЌШчЭМ1ЃЌЙ§ЕуEзїxжсЕФЦНааЯпгыХзЮяЯпНЛгкСэвЛЕуPЃЌСЌНгBEЁЂPOЃЌ
АбyЃН2ДњШыyЃНЉ![]() x2+
x2+![]() x+3ЃЌ
x+3ЃЌ
НтЕУx1ЃНЉ1ЃЌx2ЃН2
ЁрЕуPЕФзјБъЮЊЃЈЉ1ЃЌ2ЃЉЃЌ
ЁпPEЁЮOBЃЌЧвPEЃНOBЃН3ЃЌ
ЁрЫФБпаЮOBEPЪЧЦНааЫФБпаЮЃЌ
ЁрдкxжсЩЯЗНЕФХзЮяЯпЩЯЃЌДцдквЛЕуPЃЈЉ1ЃЌ2ЃЉЃЌЪЙЕУЫФБпаЮOBEPЪЧЦНааЫФБпаЮЃЛ
ЂкДцдкЃЌШчЭМ2ЃЌЩшQЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌСЌНгQAЁЂQBЁЂQEЁЂBEЃЌ
ЁпQAЃНQBЃЌ
ЁрЁїBEQЕФжмГЄЕШгкBE+QA+QEЃЌ
гжЁпBEЕФГЄЪЧЖЈжЕ
ЁрAЁЂQЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЁїBEQЕФжмГЄзюаЁЃЌ
гЩAЃЈЉ2ЃЌ0ЃЉЁЂEЃЈ2ЃЌ2ЃЉПЩЕУжБЯпAEЕФНтЮіЪНЮЊyЃН![]() x+1ЃЌ
x+1ЃЌ
ЁпХзЮяЯпЕФЖдГЦжсЪЧxЃН![]()
ЁрЕуQЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁрдкХзЮяЯпЕФЖдГЦжсЩЯЃЌДцдкЕуQЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЪЙЕУЁїBEQЕФжмГЄзюаЁЃЎ
ЃЉЃЌЪЙЕУЁїBEQЕФжмГЄзюаЁЃЎ



 ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
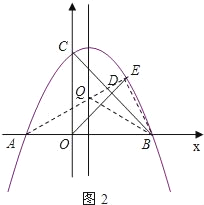
ЁОЬтФПЁПЃЈ2017СЩФўЪЁКљТЋЕКЪаЃЉШчЭМЃЌЁЯMAN=60ЁуЃЌAPЦНЗжЁЯMANЃЌЕуBЪЧЩфЯпAPЩЯвЛЖЈЕуЃЌЕуCдкжБЯпANЩЯдЫЖЏЃЌСЌНгBCЃЌНЋЁЯABCЃЈ0ЁуЃМЁЯABCЃМ120ЁуЃЉЕФСНБпЩфЯпBCКЭBAЗжБ№ШЦЕуBЫГЪБеыа§зЊ120ЁуЃЌа§зЊКѓНЧЕФСНБпЗжБ№гыЩфЯпAMНЛгкЕуDКЭЕуEЃЎ
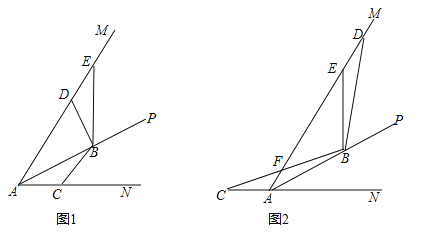
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуCдкЩфЯпANЩЯЪБЃЌЂйЧыХаЖЯЯпЖЮBCгыBDЕФЪ§СПЙиЯЕЃЌжБНгаДГіНсТлЃЛ
ЂкЧыЬНОПЯпЖЮACЃЌADКЭBEжЎМфЕФЪ§СПЙиЯЕЃЌаДГіНсТлВЂжЄУїЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуCдкЩфЯпANЕФЗДЯђбгГЄЯпЩЯЪБЃЌBCНЛЩфЯпAMгкЕуFЃЌШєAB=4ЃЌAC=![]() ЃЌЧыжБНгаДГіЯпЖЮADКЭDFЕФГЄЃЎ
ЃЌЧыжБНгаДГіЯпЖЮADКЭDFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
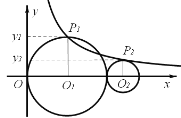
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЁбO1Й§дЕуOЃЌЧвЁбO1гыЁбO2ЯрЭтЧаЃЌдВаФO1гыO2дкxжсе§АыжсЩЯЃЌЁбO1ЕФАыОЖO1P1ЁЂЁбO2ЕФАыОЖO2P2ЖМгыxжсДЙжБЃЌЧвЕуP1![]() ЁЂP2
ЁЂP2![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЃЈx>0ЃЉЕФЭМЯѓЩЯЃЌдђ
ЃЈx>0ЃЉЕФЭМЯѓЩЯЃЌдђ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
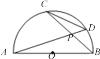
ЁОЬтФПЁПШчЭМЃЌABЪЧАыОЖЮЊ3АыдВOЕФжБОЖЃЎCDЪЧдВжаПЩвЦЖЏЕФЯвЃЌЧвCD=3ЃЌСЌНг ADЁЂBCЯрНЛгкЕуPЃЌЯвCDДгCгыAжиКЯЕФЮЛжУПЊЪМЃЌШЦзХЕуOЫГЪБеыа§зЊ120ЁуЃЌдђНЛЕуPдЫЖЏЕФТЗОЖГЄЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
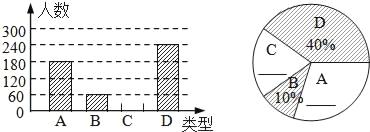
ЁОЬтФПЁПЁАДКНкЁБЪЧЮвЙњЕФДЋЭГМбНкЃЌУёМфРњРДгаГдЁАЬРдВЁБЕФЯАЫзЃЎФГЪГЦЗГЇЮЊСЫНтЪаУёЖдШЅФъЯњСПНЯКУЕФШтЯкЃЈAЃЉЁЂЖЙЩГЯк ЃЈBЃЉЁЂВЫЯкЃЈCЃЉЁЂШ§ЖЁЯк ЃЈDЃЉЫФжжВЛЭЌПкЮЖЬРдВЕФЯВАЎЧщПіЃЌдкНкЧАЖдФГОгУёЧјЪаУёНјааСЫГщбљЕїВщЃЌВЂНЋЕїВщЧщПіЛцжЦГЩШчЯТСНЗљЭГМЦЭМЃЈЩаВЛЭъећЃЉЃЎЧыИљОнвдЩЯаХЯЂЛиД№ЃК
ЃЈ1ЃЉБОДЮВЮМгГщбљЕїВщЕФОгУёШЫЪ§ЪЧЁЁ ЁЁШЫЃЛ
ЃЈ2ЃЉНЋЭМ ЂйЂкВЙГфЭъећЃЛЃЈ жБНгВЙЬюдкЭМжаЃЉ
ЃЈ3ЃЉЧѓЭМЂкжаБэЪОЁАAЁБЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉШєОгУёЧјга8000ШЫЃЌЧыЙРМЦАЎГдDЬРдВЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛВЛЭИУїЕФВМДќРяЃЌзАгаКьЁЂЛЦЁЂРЖШ§жжбеЩЋЕФаЁЧђЃЈГ§беЩЋЭтЦфгрЖМЯрЭЌЃЉЃЌЦфжагаКьЧђ2ИіЃЌРЖЧђ1ИіЃЌЛЦЧђШєИЩИіЃЌЯжДгжаШЮвтУўГівЛИіЧђЪЧКьЧђЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓПкДќжаЛЦЧђЕФИіЪ§ЃЛ
ЃЈ2ЃЉМзЭЌбЇЯШЫцЛњУўГівЛИіаЁЧђЃЈВЛЗХЛиЃЉЃЌдйЫцЛњУўГівЛИіаЁЧђЃЌЧыгУЁАЪїзДЭМЗЈЁБЛђЁАСаБэЗЈЁБЃЌ
ЧѓСНДЮУў ГіЖМЪЧКьЧђЕФИХТЪЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOAЃЌOBЪЧЁбOЕФСНЬѕАыОЖЃЌOAЁЭOBЃЌCЪЧАыОЖOBЩЯЕФвЛЖЏЕуЃЌСЌНгACВЂбгГЄНЛЁбOгкDЃЌЙ§ЕуDзїжБЯпНЛOBбгГЄЯпгкEЃЌЧвDE=CEЃЌвбжЊOA=8ЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЕБЁЯA=30ЁуЪБЃЌЧѓCDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
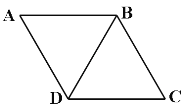
ЁОЬтФПЁПдкСтаЮABCDжаЃЌBD=BCЃЌ
ЃЈ1ЃЉШчЭМЃЌШєСтаЮABCDЕФУцЛ§ЮЊ6![]() ЃЎЧѓЕуBЕНDCЕФзюЖЬОрРы.
ЃЎЧѓЕуBЕНDCЕФзюЖЬОрРы.
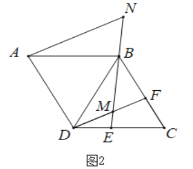
ЃЈ2ЃЉШчЭМ2ЃЌЕуFдкBCБпЩЯЃЌЧвDEЃНCFЃЌСЌНгDFНЛBEгкЕуMЃЌСЌНгEBВЂбгГЄжСЕуNЃЌЪЙЕУBNЃНDMЃЌЧѓжЄЃКANЃНDM+BMЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
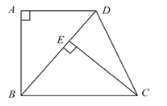
ЁОЬтФПЁПШчЭМЃЌвбжЊRtЁїABDжаЃЌЁЯAЃН90ЁуЃЌНЋаББпBDШЦЕуBЫГЪБеыЗНЯђа§зЊжСBCЃЌЪЙBCЁЮADЃЌЙ§ЕуCзїCEЁЭBDгкЕуEЃЎ
(1)ЧѓжЄЃКЁїABDЁеЁїECBЃЛ
(2)ШєЁЯABDЃН30ЁуЃЌBE=3ЃЌЧѓЛЁCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com