
【题目】如图所示,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (元,分别用y1与y2表示)与照明时间
(元,分别用y1与y2表示)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(1)根据图象分别求出![]() ,
,![]() 对应的函数(分别用y1与y2表示)关系式;
对应的函数(分别用y1与y2表示)关系式;
(2)对于白炽灯与节能灯,请问该选择哪一种灯,使用费用会更省?

【答案】(1)y1=![]() x+2,y2=
x+2,y2=![]() x+20(2)见解析
x+20(2)见解析
【解析】
(1)由图像可知,l1的函数为一次函数,则设y1=k1x+b1.由图象知,l1过点(0,2)、(500,17),能够得出l 1的函数解析式.同理可以得出l2的函数解析式.
(2)由图像可知l1、 l2的图像交于一点,那么交点处白炽灯和节能灯的费用相同,即![]() x+2=
x+2=![]() x+20,由此得出x=1000时费用相同;x<1000时,使用白炽灯省钱;x>1000时,使用节能灯省钱.
x+20,由此得出x=1000时费用相同;x<1000时,使用白炽灯省钱;x>1000时,使用节能灯省钱.
(1)设l1的函数解析式为y1=k1x+b1,
由图象知,l1过点(0,2)、(500,17),
可得方程组 ,解得
,解得 ,
,
故,l1的函数关系式为y1=![]() x+2;
x+2;
设l2的函数解析式为y2=k2x+b2,
由图象知,l2过点(0,20)、(500,26),
可得方程组 ,解得
,解得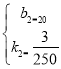 ,
,
y2=![]() x+20;
x+20;
(2)由题意得,![]() x+2=
x+2=![]() x+20,解得x=1000,
x+20,解得x=1000,
故,①当照明时间为1000小时时,两种灯的费用相同;
②当照明时间超过1000小时,使用节能灯省钱.
③当照明时间在1000小时以内,使用白炽灯省钱.


科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点O叠放在一起。
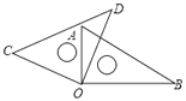
(1)若∠AOD=25°,则∠AOC= 65° ,∠BOD= ,∠BOC= ;
(2)比较∠AOC与∠BOD的大小关系,并说明理由;
(3)猜想∠AOD与∠BOC的数量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC,BD相交于O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论

①BE⊥AC
②四边形BEFG是平行四边形
③EG=GF
④EA平分∠GEF
其中正确的是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,17,4分)已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .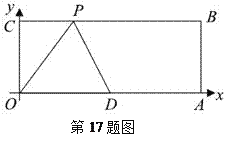
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a、b、c满足abc>0,求![]() 的值.
的值.
(解决问题)由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即a>0,b>0,c>0时,
则:![]() =
=![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个为负数时,设a>0,b<0,c<0,
即:![]() =
=![]() =1+(1)+(1)=1,所以
=1+(1)+(1)=1,所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)已知a<0,b>0,c>0,则![]() ,
,![]() ,
,![]() ;
;
(2)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(3)已知|a|=3,|b|=1,且a<b,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(x1,y1),(x2,y2),(x3,y3)都在函数y=-2x+7的图象上,若数据x1,x2,x3的方差为5,则另一组数据y1,y2,y3的方差为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com