
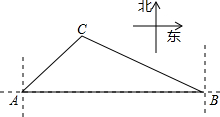
 如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.
如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.分析 (1)过C作AB的垂线,设垂足为D,则CD的长为海轮在航行过程中与灯塔C的最短距离;
(2)在Rt△BCD中,根据60°角的余弦值即可求出海轮在B处时与灯塔C的距离.
解答  解:(1)过C作AB的垂线,垂足为点D,
解:(1)过C作AB的垂线,垂足为点D,
根据题意可得:∠1=∠2=45°,∠3=∠4=60°,
设CD的长为x海里,
在Rt△ACD中,tan45°=$\frac{AD}{CD}$,则AD=CD=x,
在Rt△BCD中,tan60°=$\frac{BD}{CD}$,则BD=$\sqrt{3}$x,
∵AB=80,
∴AD+BD=80,
∴x+$\sqrt{3}$x=80,
解得:x=40$\sqrt{3}$-40,
答:海轮在航行过程中与灯塔C的最短距离是(40$\sqrt{3}$-40)海里;
(2)在Rt△BCD中,cos60°=$\frac{CD}{BC}$,
∴BC=2CD=80$\sqrt{3}$-80(海里),
答:海轮在B处时与灯塔C的距离为(80$\sqrt{3}$-80)海里.
点评 本题主要考查解直角三角形的应用-方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


科目:初中数学 来源: 题型:填空题
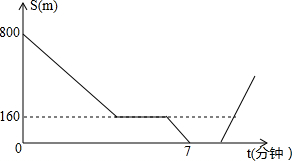 在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.
在一次集训中,一支队伍出发20分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后维续按原速原路返回,在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象,若传达命令所花时间都为2分钟.则当通讯员再次回到队尾时.他一共走了$\frac{3880}{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
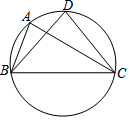 如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )
如图,A、B、C三点在圆上,在△ABC中,∠ABC=70°,∠ACB=30°,D是弧BAC的中点,连结DB,DC,则∠DBC的度数为( )| A. | 70° | B. | 50° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com