
分析 (1)根据题意可以列出相应的方程,从而可以解答本题;
(2)根据题意可以列出相应的不等式,从而可以得到有多少种购买方案和哪种方案,最省钱.
解答 解:(1)设购买铁撮子的单价为x元,
3(1.5x-2)=4x,
解得,x=12,
1.5x-2=16
即扫帚、铁撮子两种工具的单价各是16元,12元;
(2)设购买铁撮子a把,
$\left\{\begin{array}{l}{12a+16(100-a)≤1440}\\{100-a≥50}\\{100-a≤3a}\end{array}\right.$,
解得,40≤a≤50,
∴有11种购买方案,
花费为:12a+16(100-a)=-4a+1600,
∴当a=50时,花费最少,此时,-4a+1600=-4×50+1600=1400,
即当购买买铁撮子50把,扫帚50把时最省钱.
点评 本题考查一次函数的应用、一元一次方程的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题条件,利用方程和不等式的思想解答问题.


科目:初中数学 来源: 题型:解答题
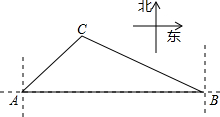 如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.
如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
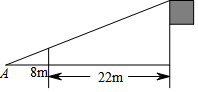 如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )
如图,为测量学校旗杆的高度,小东用长为3.2m的竹竿做测量工具,移动竹竿使竹竿和旗杆两者顶端的影子恰好落在地面的同一点A,此时,竹竿与点A相距8m,与旗杆相距22m,则旗杆的高为( )| A. | 6m | B. | 8.8m | C. | 12m | D. | 30m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
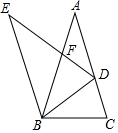 如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.
如图,已知△ABC与△BED都是顶角为36°的等腰三角形,点D是边AC上一点,且满足BC2=CD•AC,DE与AB相交于点F,则图中有( )对相似三角形.| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com