
点A,B,C都在半径为r的圆上,直线AD⊥直线BC,垂足为D,直线BE⊥直线AC,垂足为E,直线AD与BE相交于点H,若 ,则∠ABC所对的弧长等于 (长度单位).
,则∠ABC所对的弧长等于 (长度单位).
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:填空题
过点(-1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线 平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 .
平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感。他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证: .
.
证明:连结DB,过点D作BC边上的高DF,
则DF=EC=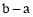 ,
,
∵  ,
,
又∵ ,
,
∴ ,
,
∴
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证: .
.
证明:连结 ,
∵ ,
,
又∵ ,
,
∴ .
∴  .
.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:解答题
在直角坐标系中,设x轴为直线l,函数 的图像分别是
的图像分别是 ,半径为1的
,半径为1的 与直线
与直线 中的两条相切,例如
中的两条相切,例如 是其中一个
是其中一个 的圆心坐标.
的圆心坐标.
(1)写出其余满足条件的 的圆心坐标;
的圆心坐标;
(2)在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:选择题
已知边长为a的正方形面积为8,则下列关于a的说法中,错误的是( )
A. a是无理数 B.a是方程 的解
的解
C.a是8的算术平方根 D.a满足不等式组
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏镇江卷)数学(解析版) 题型:解答题
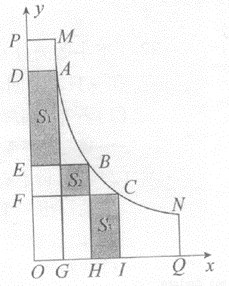
六•一儿童节,小文到公园游玩,看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积相等,比如:A、B、C是弯道MN上任三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等. 爱好数学的他建立了平面直角坐标系(如图).图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米),OG=GH=HI.
(1)求S1和S3的值;
(2)设T 是弯道MN上的任一点,写出y关于x的函数关系式;
是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改选,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com