
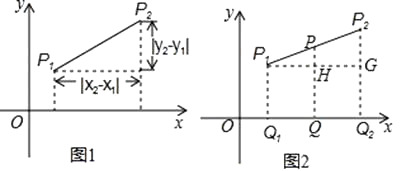
【题目】小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= ![]() 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x=
他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ![]() ,y=
,y= ![]() .
.
(1)请你帮小明写出中点坐标公式的证明过程;
(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)如图3,点P(2,n)在函数y= ![]() x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.
x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.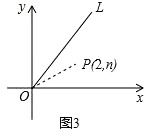
【答案】
(1)
证明:∵P1(x1,y1),P2(x2,y2),
∴Q1Q2=OQ2﹣OQ1=x2﹣x1,
∴Q1Q= ![]() ,
,
∴OQ=OQ1+Q1Q=x1+ ![]() =
= ![]() ,
,
∵PQ为梯形P1Q1Q2P2的中位线,
∴PQ= ![]() =
= ![]() ,
,
即线段P1P2的中点P(x,y)P的坐标公式为x= ![]() ,y=
,y= ![]()
(2) ![]() ;(﹣3,3)或(7,1)或(﹣1,﹣3)
;(﹣3,3)或(7,1)或(﹣1,﹣3)
(3)
解:如图,设P关于直线OL的对称点为M,关于x轴的对称点为N,连接PM交直线OL于点R,连接PN交x轴于点S,连接MN交直线OL于点E,交x轴于点F,
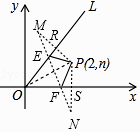
又对称性可知EP=EM,FP=FN,
∴PE+PF+EF=ME+EF+NF=MN,
∴此时△PEF的周长即为MN的长,为最小,
设R(x, ![]() x),由题意可知OR=OS=2,PR=PS=n,
x),由题意可知OR=OS=2,PR=PS=n,
∴ ![]() =2,解得x=﹣
=2,解得x=﹣ ![]() (舍去)或x=
(舍去)或x= ![]() ,
,
∴R( ![]() ,
, ![]() ),
),
∴ ![]() =n,解得n=1,
=n,解得n=1,
∴P(2,1),
∴N(2,﹣1),
设M(x,y),则 ![]() =
= ![]() ,
, ![]() =
= ![]() ,解得x=
,解得x= ![]() ,y=
,y= ![]() ,
,
∴M( ![]() ,
, ![]() ),
),
∴MN= ![]() =
= ![]() ,
,
即△PEF的周长的最小值为 ![]()
【解析】(2)①∵M(2,﹣1),N(﹣3,5),
∴MN= ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;
②∵A(2,2),B(﹣2,0),C(3,﹣1),
∴当AB为平行四边形的对角线时,其对称中心坐标为(0,1),
设D(x,y),则x+3=0,y+(﹣1)=2,解得x=﹣3,y=3,
∴此时D点坐标为(﹣3,3),
当AC为对角线时,同理可求得D点坐标为(7,1),
当BC为对角线时,同理可求得D点坐标为(﹣1,﹣3),
综上可知D点坐标为(﹣3,3)或(7,1)或(﹣1,﹣3),
所以答案是:(﹣3,3)或(7,1)或(﹣1,﹣3);
【考点精析】根据题目的已知条件,利用勾股定理的概念和轴对称-最短路线问题的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点A(3,0),B(2,﹣3),C(0,﹣3)
(1)求抛物线的表达式;
(2)设点D是抛物线上一点,且点D的横坐标为﹣2,求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
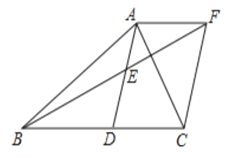
【题目】如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此 规律,倍长n次后得到的△A2016B2016C2016的面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )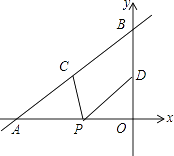
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点;过点
的中点;过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 分别满足什么条件时,四边形
分别满足什么条件时,四边形![]() 是菱形;四边形
是菱形;四边形![]() 是矩形,并说明理由.
是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=![]() 位于第一象限的图象上,则k的值为( )
位于第一象限的图象上,则k的值为( )
A.9![]()
B.9![]()
C.3![]()
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,A.B两点的坐标分别为(﹣2,2),(1,8),
(1)求△ABO的面积.
(2)若y轴上有一点M,且△MAB的面积为10.求M点的坐标.
(3)如图,把直线AB以每秒2个单位的速度向右平移,运动t秒钟后,直线AB过点F(0,﹣2),此时A点的坐标为 ,B点的坐标为 ,过点A作AE⊥y轴于点E,过点B作BD⊥y轴于点D,请根据S△FBD=S△FAE+S梯形ABDE,求出满足条件的运动时间t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com