Question

11．已知：如图①，在矩形ABCD中，AB=2，AD=$\frac{8}{3}$．过A作AH⊥BD于H．
（1）将△AHB沿AB翻折，得△AEB．求证：∠EAB=∠ADB；
（2）如图②，将△ABE绕点B顺时针旋转，记旋转中的△ABE为△A′BE′，在旋转过程中，延长A′E′与对角线BD交于点Q，与直线AD交于点P，问是否存在这样的Q、P两点，使△DQP为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．

Answer 1

分析 （1）根据折叠的性质和等角的余角相等即可证明；
（2）分类讨论，分三种情况①PD=DQ，②PQ=PD，③QP=QD．

解答 （1）证明：由翻折可知：∠EAB=∠BAH．
∵∠BAH+∠DAH=∠DAH+∠ADB=90°．
∴∠BAH=∠ADB，
∴∠EAB=∠ADB．   
（2）如图①所示，当PD=DQ时，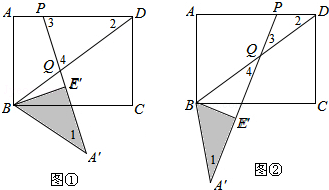
在矩形ABCD中，AB=2，AD=$\frac{8}{3}$，
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\frac{10}{3}$，
∴AH=$\frac{AB×AD}{BD}$=$\frac{8}{5}$，BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\frac{6}{5}$
由折叠得，AE=AH=$\frac{8}{5}$，BE=BH=$\frac{6}{5}$，
由旋转得，A'E'=AE=$\frac{8}{5}$，BE'=BE=$\frac{6}{5}$
∵∠1=∠2，
∴∠A′BQ=∠A′QB，
∴A′Q=A′B=AB=2，
∴E′Q=A'B-A'E'=$\frac{2}{5}$．
在Rt△E′BQ中，BQ=$\sqrt{E'{B}^{2}+E'{Q}^{2}}$=$\frac{2\sqrt{10}}{5}$．
∴DQ=BD-BQ=$\frac{10}{3}$-$\frac{2\sqrt{10}}{5}$．
如图②所示，当PQ=PD，
由∠1=∠2可得∠1=∠4，
∴BQ=A′B=2，
∴DQ=BD-BQ=$\frac{10}{3}$-2=$\frac{4}{3}$．
当QP=QD时，如图3，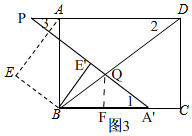
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
∴AD∥BA'，
∴点A'在BC上，
∴∠2=∠A'BQ=∠1，
∴BQ=A'Q，
过点Q作QF⊥A'B，
∴BF=$\frac{1}{2}$A'B=1，
∵tan∠A'BQ=tan∠2=$\frac{AB}{AD}$=$\frac{3}{4}$=$\frac{FQ}{BF}$=$\frac{FQ}{1}$，
∴FQ=$\frac{3}{4}$，
∴BQ=$\frac{5}{4}$，
∴DQ=BD-BQ=$\frac{10}{3}$-$\frac{5}{4}$=$\frac{25}{12}$
综上可知：当DQ=$\frac{10}{3}-\frac{2\sqrt{10}}{5}$或$\frac{4}{3}$或$\frac{25}{12}$时，△DPQ是等腰三角形．

点评 此题是几何变换综合题，主要考查了翻折的性质、矩形的性质、等腰三角形的判定与性质、勾股定理以及分类讨论的数学方法的综合运用，第（2）小题根据题意画出图形，分类讨论各种情况是解决问题的关键．