
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,
,![]() (
(![]() 在
在![]() 左侧),与
左侧),与![]() 轴正半轴交于点
轴正半轴交于点![]() ,点
,点![]() 在抛物线上,
在抛物线上,![]() 轴,且
轴,且![]() .
.
(1)求点![]() ,
,![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)点![]() 为
为![]() 轴右侧抛物线上一点.
轴右侧抛物线上一点.
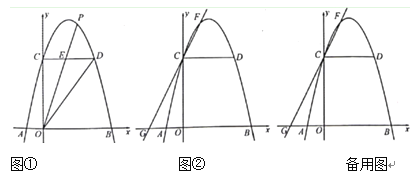
①如图①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
②如图②,抛物线上一点![]() 的横坐标为2,直线
的横坐标为2,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)令y=0,解方程即可求出点A、B的坐标,由此可求得AB的长及对称轴,再根据![]() 即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
即可求得OD长,根据对称轴即可求得CD=6,再根据勾股定理即可求得点C坐标,将点C坐标代入函数关系式从而可求得a的值;
(2)①作![]() 于
于![]() ,根据
,根据![]() 平分
平分![]() 可得
可得![]() ,进而设
,进而设![]() ,根据
,根据![]() 可得方程
可得方程![]() 求解即可求得点E坐标为
求解即可求得点E坐标为![]() ,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
,再用待定系数法求得直线OP的函数关系式,与二次函数关系式联立方程组即可求得点P坐标;
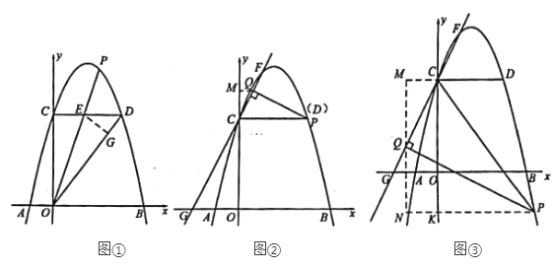
②分两种情形(Ⅰ)若点![]() 在
在![]() 点上方,如图②,(Ⅱ)若点
点上方,如图②,(Ⅱ)若点![]() 在点
在点![]() 下方,如图③,分别列出方程即可解决.
下方,如图③,分别列出方程即可解决.
解:(1)令![]() ,则
,则![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]()
∴![]() ,
,
∵点C在y轴上且![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①作![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
设![]() 对应函数表达式为
对应函数表达式为![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
∴![]() 对应函数表达式为
对应函数表达式为![]() .
.
∵![]() ,
,
∴二次函数表达式为![]() ,
,
∴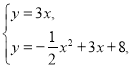 ,
,
解得![]() 或
或![]() (舍去)
(舍去)
∴点![]() .
.
②∵当![]() 时,
时,![]() ,∴点
,∴点![]() .
.
设直线![]() 的函数表达式为
的函数表达式为![]()
把点![]() 、点
、点![]() 代入,
代入,
得![]()
解得![]()
∴直线![]() 的函数表达式为
的函数表达式为![]() ,
,
∴点![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅰ)若点![]() 在
在![]() 点上方,如图②.
点上方,如图②.
过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() .
.
∵![]() ,
,
∴![]() 轴,
轴,
∵![]() 轴,
轴,
∴点![]() 与点
与点![]() 重合,
重合,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴![]() .
.
把![]() 代入
代入![]()
得,![]() .
.
∴![]() .
.
(Ⅱ)若点![]() 在点
在点![]() 下方,如图③.
下方,如图③.
过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 轴于点
轴于点![]() .
.
∴![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]()
∵![]() 轴,
轴,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴设![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() ,得
,得
![]() ,
,
∴![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
代入![]() 得
得
![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 为
为![]() 的中点,一块足够大的三角板的直角顶点与点
的中点,一块足够大的三角板的直角顶点与点![]() 重合,将三角板绕点
重合,将三角板绕点![]() 旋转,三角板的两直角边分别交
旋转,三角板的两直角边分别交![]() 或它们的延长线)于点
或它们的延长线)于点![]() ,设
,设![]() ,下列四个结论:①
,下列四个结论:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
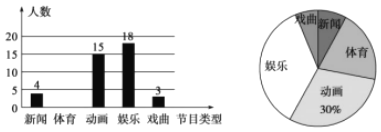
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
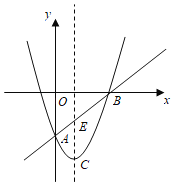
【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 与直线
与直线![]() 都经过
都经过![]() 、
、![]() 两点,该抛物线的顶点为C.
两点,该抛物线的顶点为C.
(1)求此抛物线和直线![]() 的解析式;
的解析式;
(2)设直线![]() 与该抛物线的对称轴交于点E,在射线
与该抛物线的对称轴交于点E,在射线![]() 上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
(3)设点P是直线![]() 下方抛物线上的一动点,当
下方抛物线上的一动点,当![]() 面积最大时,求点P的坐标,并求
面积最大时,求点P的坐标,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,对“垃圾分类”的知晓情况分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.其中,
四类.其中,![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
“垃圾分类”知晓情况各类别人数条形统计图 “垃圾分类”知晓情况各类别人数扇形统计图
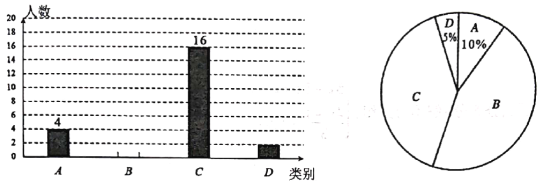
根据以上信息解决下列问题:
(1)初三(1)班参加这次调查的学生有______人,扇形统计图中类别![]() 所对应扇形的圆心角度数为______°;
所对应扇形的圆心角度数为______°;
(2)求出类别![]() 的学生数,并补全条形统计图;
的学生数,并补全条形统计图;
(3)类别![]() 的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某市出台了民生兜底、医保脱贫、教育教助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为![]() 类贫困户。为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
类贫困户。为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
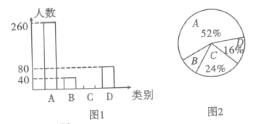
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户;
(2)抽查了多少户![]() 类贫困户?并补全统计图;
类贫困户?并补全统计图;
(3)若该地共有1300户贫困户,请估计至少得到4项帮扶措施的大约有多少户;
(4)为更好地做好精准扶贫工作,现准备从![]() 类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
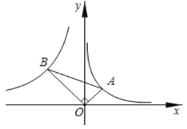
【题目】如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y=![]() (x>0)与y=
(x>0)与y=![]() (x<0)的图象上,则tan∠BAO的值为 ____.
(x<0)的图象上,则tan∠BAO的值为 ____.
查看答案和解析>>
科目:初中数学 来源: 题型:
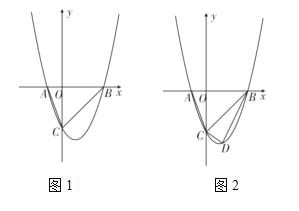
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于A、B两点,(点A在点B的左侧)与y轴交于点C,连接AC.
轴于A、B两点,(点A在点B的左侧)与y轴交于点C,连接AC.
(1)求点A、点B和点C的坐标;
(2)若点D为第四象限内抛物线上一动点,点D的横坐标为m,△BCD的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)抛物线的对称轴上是否存在点P,使△BCP为等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
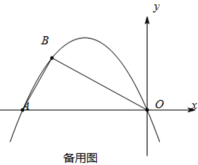
【题目】如图,在平面直角坐标系中,O是坐标原点,抛物线![]() 经过A(-5,0),
经过A(-5,0), 两点,连接AB,BO.
两点,连接AB,BO.
(1)求抛物线表达式;
(2)点C是第三象限内的一个动点,若△AOC与△AOB全等,请直接写出点C坐标______;
(3)若点D从点O出发沿线段OA向点A作匀速运动,速度为每秒1个单位长度,同时线段OA上另一个点H从点A出发沿线段AO向点O作匀速运动,速度为每秒2个单位长度(当点H到达点O时,点D也同时停止运动).过点D作x轴的垂线,与直线OB交于点E,延长DE到点F,使得EF=DE,以DF为边,在DF左侧作等边三角形DGF(当点D运动时,点G、点F也随之运动).过点H作x轴的垂线,与直线AB交于点L,延长HL到点M,使得LM=HL,以HM为边,在HM的右侧作等边三角形HMN(当点H运动时,点M、点N也随之运动).当点D运动t秒时,△DGF有一条边所在直线恰好过△HMN的重心,直接写出此刻t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com