
【题目】△![]() 中,
中, ![]() .取
.取![]() 边的中点
边的中点![]() ,作
,作![]() ⊥
⊥![]() 于点
于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() 交于点
交于点![]() .
.
(1)如图1,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并求
并求![]() 的值;
的值;
(2)如图2,如果![]() ,求证:
,求证: ![]() ⊥
⊥![]() 并用含
并用含![]() 的式子表示
的式子表示![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=![]() ∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=
∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=![]() BC2DF=BCDF,即
BC2DF=BCDF,即![]() ,由此可证到△AFD∽△BEC,则有
,由此可证到△AFD∽△BEC,则有![]() ,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-
,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,从而可得
,从而可得![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
试题解析:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC=![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴![]() ,
,
即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD=![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═![]() BC2DF=BCDF,
BC2DF=BCDF,
∴![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴![]() ,
,
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-![]() ∠BAC,BD=
∠BAC,BD=![]() BC,
BC,
∴tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,
,
∴![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°,
(1)如图1,
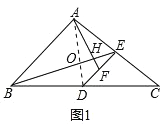
根据以上结论可得:
∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() ×90°)=
×90°)=![]() ;
;
∴AF⊥BE, ![]() =
=![]() ;
;
(2)如图2,
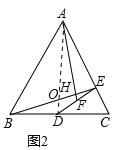
根据以上结论可得:∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() α);
α);
∴AF⊥BE, ![]() =
=![]() tan(90°-
tan(90°-![]() α).
α).


科目:初中数学 来源: 题型:
【题目】如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.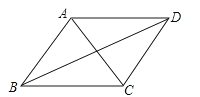
A.①③
B.②③
C.③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年参加我市初中毕业生学业考试的总人数约为56000人,这个数据用科学记数法表示为( )
A.5.6×103
B.5.6×104
C.5.6×105
D.0.56×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
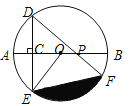
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,D为BC的中点,以下结论:①△ABD≌△ACD;②AB=AC;③∠B=∠C;④AD是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com