
����Ŀ�����Ķ����н����̣�Ȼ���ٽ��⣮
������֪����ʽ2x3��x2+m��һ����ʽ��2x+1����m��ֵ��
�ⷨһ����2x3��x2+m����2x+1����x 2+ax+b����
��2x 3��x2+m��2x 3+��2a+1��x2+��a+2b��x+b��
�Ƚ�ϵ���� �����
����� ����m��
����m��![]() ��
��
�ⷨ������2x3��x2+m��A��2x+1����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ���������ȡx����![]() ��2��������3��������2+m��0����m��
��2��������3��������2+m��0����m��![]() ��
��
��1����֪����ʽ2x3��2x2+ m��һ����ʽ��x+2����m��ֵ��
��2����֪x 4+ m x3+ n x��16����ʽ��x��1���ͣ�x��2������m��n��ֵ��
���𰸡���1��m��24����2��m����5��n��20��
��������
��1����2x3��2x2+m��A��x+2����AΪ��ʽ���������Ǻ��ʽ����ȡx=-2�����뼴�ɽ��
��2����x4+mx3+nx��16��A��x��1����x��2����AΪ��ʽ���������Ǻ��ʽ����ȡx=1��x=2�����뼴�ɽ��
�⣺��1���߶���ʽ2x3��2x2+m��һ����ʽ��x+2��
����2x3��2x2+m��A��x+2����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ�������ȡx����2��
2������2��3��2������2��2+m��0����m��24��
��2����x4+mx3+nx��16����ʽ��x��1���ͣ�x��2����
����x4+mx3+nx��16��A��x��1����x��2����AΪ��ʽ��
������ʽΪ���ʽ��Ϊ�������ȡx��2��x��1��
����ã�24+m��23+2n��16��0��14+m��13+n��16��0��
��ã�m����5��n��20��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC��D���߶�BC���ӳ�����һ�㣬��ADΪһ����AD���Ҳ�����ADE��ʹAE=AD����DAE=��BAC������CE��
��1����ͼ1����D���߶�BC���ӳ������ƶ�������BAC=30��������DCE=�� ����
��2������BAC=������DCE=�£�
����ͼ1������D���߶�BC���ӳ������ƶ�ʱ��������֮����ʲô������ϵ����˵�����ɣ�
������D��ֱ��BC�ϣ�����B��C�غϣ��ƶ�ʱ��������֮����ʲô������ϵ����ֱ��д����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����E��ֱ��AB��CD�ڲ�һ�㣬AB��CD������EA��ED��
��1��̽����
������A=30�㣬��D=40�㣬���AED���ڶ��ٶȣ�
������A=20�㣬��D=60�㣬���AED���ڶ��ٶȣ�
����ͼ��1���С�AED����EAB����EDC��ʲô������ϵ����֤����Ľ��ۣ�
��2����չ����ͼ��2��������FE�����ABCD�ı�AB���ڵ�E�����CD���ڵ�F���٢ڢֱܷۢ��DZ�����FE�������ĸ��������߽磬���Тۢ�λ��ֱ��AB���Ϸ�����P��λ�������ĸ������ϵ㣬���룺��PEB����PFC����EPF֮��Ĺ�ϵ������Ҫ��֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD��ƽ��ֱ������ϵ�У�AD=6����OA��OB�ij��ǹ��� ![]() ��һԪ���η���
��һԪ���η��� ![]() ������������OA��OB
������������OA��OB
��1����cos��ABC��ֵ��
��2����EΪx���ϵĵ㣬�� ![]() �������E�����꣬���жϡ�AOE���DAO�Ƿ����ƣ���˵������
�������E�����꣬���жϡ�AOE���DAO�Ƿ����ƣ���˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��������������ֱ�ΪA (3. 3)��B (-3, 0), C (0. -2)��
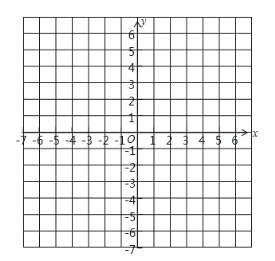
��1���������ƽ��ֱ������ϵ�зֱ����A��B, C���㣬��������ABC��
��2����(1)�еġ�ABC����ƽ��3����λ���ȣ���������2����λ���ȣ��õ���![]() ��ͼ�л�����
��ͼ�л�����![]() ����ֱ�д��A1��B1��C1��������꣮
����ֱ�д��A1��B1��C1��������꣮
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ܷ���AB��25�ף���ͼ��ʾ��б����һ���ϣ�

��1�������ӵ���ǽ7�ף�������ӵĶ��˾�����ж�ߣ�
��2���ڣ�1���������£�������ӵĶ����»���4�ף���ô���ӵĵ���ˮƽ�����˼��ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ķ���ֽ�У�ÿ��С�����DZ߳�Ϊ1����λ�������Σ�ͼ�١�ͼ�ڡ�ͼ�۾�Ϊ���㶼�ڸ���ϵ������Σ�ÿ��С����Ķ���и�㣩��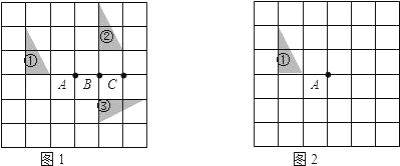
��1����ͼ1�У�ͼ�پ���һ���任���ƽ�ơ�����ת������Գơ������Եõ�ͼ�ڣ�
��2����ͼ1�У�ͼ���ǿ�����ͼ�ھ���һ����ת�任�õ��ģ�����ת�����ǵ����A���� ��B����C������
��3����ͼ2�л���ͼ���Ƶ�A˳ʱ����ת90����ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ������һ����
������һ����![]() ��
��![]() ��������
��������![]() �����˶�����
�����˶�����![]() �ij���
�ij���![]() ��ʱ��
��ʱ��![]() ֮��Ĺ�ϵ��ͼ���ʾ�����ǣ� ��
֮��Ĺ�ϵ��ͼ���ʾ�����ǣ� ��

A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com