
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
分析 (1)利用待定系数法求一次函数解析式即可得出答案;
(2)首先假设一张薄板的利润为p元,它的成本价为mx2元,由题意,得:W=y-mx2,进而得出m的值,求出函数解析式即可;
(3)利用二次函数的最值公式求出二次函数的最值即可.
解答 解:(1)设一张薄板的边长为x cm,它的出厂价为y元,基础价为n元,浮动价为kx元,
则y=kx+n
由表格中数据得$\left\{\begin{array}{l}0=3k+n\\ 4=k+n\end{array}\right.$,
解得$\left\{\begin{array}{l}k=-2\\ n=6\end{array}\right.$∴,
y=2x+10;
(2)设它的成本价为mx2元,由题意,得:
p=y-mx2=2x+10-mx2,
将x=40,p=26代入p=2x+10-mx2中,
得26=2×40+10-m×402.
解得:m=$\frac{1}{25}$.
所以p=-$\frac{1}{25}$x2+2x+10.
(3)当P=34时,-$\frac{1}{25}$x2+2x+10=34,
解得:x1=20,x2=30(舍去),
所以一张薄板的利润是34元,且成本最低时薄板的边长为20cm;
∵p=-$\frac{1}{25}$x2+2x+10=-$\frac{1}{25}$(x-25)2+35,
∴当薄板的边长为25cm时,所获利润最大,最大值35元.
点评 本题考查了二次函数的最值求法以及待定系数法求一次函数解析式,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5a2+3a2=8a4 | B. | a3•a4=a12 | C. | (a+2b)2=a2+4b2 | D. | -$\root{3}{125}$=-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
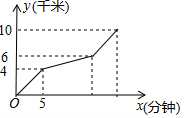 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )
如图,点A是抛物线y=a(x-3)2+k与y轴的交点,AB∥x轴交抛物线另一点于B,点C为该抛物线的顶点,若△ABC为等边三角形,则a值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
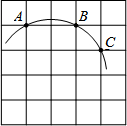 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.
如图,在5×5正方形网格中,一条圆弧经过A,B,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -1.5 | C. | $-\sqrt{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com