
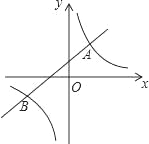
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)相交于A(1,2),B(n,-1)两点.
(m≠0)相交于A(1,2),B(n,-1)两点.
(1)求双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式kx+b<![]() 的解集.
的解集.
【答案】(1)y=![]() ;(2)y2>y3>y1;(3)x<-2或0<x<1.
;(2)y2>y3>y1;(3)x<-2或0<x<1.
【解析】
试题(1)根据待定系数法即可求得;
(2)根据反比例函数的性质即可判断;
(3)根据图象的交点坐标即可得到不等式kx+b<![]() 的解集.
的解集.
试题解析:(1)∵双曲线y=![]() 经过点A(1,2),
经过点A(1,2),
∴m=2,
∴双曲线的解析式为y=![]() ;
;
(2)根据反比例函数的图象在一、三象限y随x的增大而减小可知:若x1<0<x2<x3,则y2>y3>y1;
(3)∵点B(n,-1)在双曲线y=![]() 上,
上,
∴n=-2,
∴B点坐标为(-2,-1)
A(1,2)、B(-2,-1)在直线y=kx+b上,
∴![]() ,
,
解得![]() .
.
∴直线的解析式为y=x+1.
根据图象得当x<-2或0<x<1时,kx+b<![]() ,
,
即不等式kx+b<![]() 的解集为:x<-2或0<x<1.
的解集为:x<-2或0<x<1.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】为支援困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(1)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共1000件,且总费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() .
.
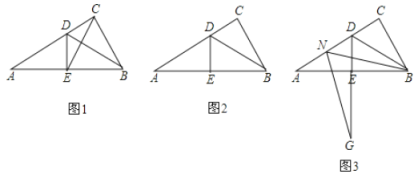
(1)如图![]() ,连接
,连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)点![]() 是线段
是线段![]() 上的一点(不与点
上的一点(不与点![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,请你在图
,请你在图![]() 中画出完整图形,并直接写出
中画出完整图形,并直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究
,试探究![]() 与
与![]() 数量之间的关系,并说明理由.
数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
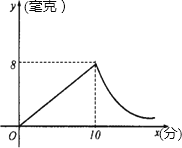
【题目】为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分钟)成正比例;燃烧阶段后,y与x成反比例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:
(1)求药物燃烧时y与x的函数解析式.
(2)求药物燃烧阶段后y与x的函数解析式.
(3)当“药熏消毒”时间到50分钟时,每立方米空气中的含药量对人体方能无毒害作用,那么当“药熏消毒”时间到50分钟时每立方米空气中的含药量为多少毫克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的![]() ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
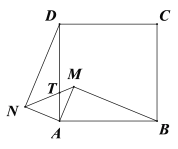
【题目】如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN.
(1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若AT=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
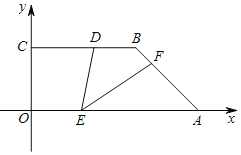
【题目】如图,BC⊥y轴,BC<OA,点A,点C分别在x轴、y轴的正半轴上,D是线段BC上一点,BD=![]() OA=
OA=![]() ,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A. 4,3B. 6,3C. 3,4D. 6,5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com