
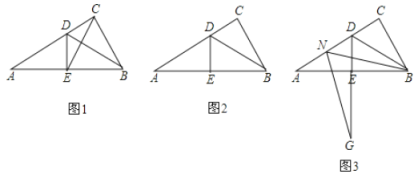
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() .
.
(1)如图![]() ,连接
,连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)点![]() 是线段
是线段![]() 上的一点(不与点
上的一点(不与点![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,请你在图
,请你在图![]() 中画出完整图形,并直接写出
中画出完整图形,并直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究
,试探究![]() 与
与![]() 数量之间的关系,并说明理由.
数量之间的关系,并说明理由.
【答案】(1)证明见解析;(2)AD=DG+DM;(3)AD=DGDN;理由见解析.
【解析】
(1)如解题所示,根据直角三角形的性质可得∠ABC=60°,BC=![]() ,然后根据等角对等边可得DA=DB,再根据三线合一可得AE=BE=
,然后根据等角对等边可得DA=DB,再根据三线合一可得AE=BE=![]() ,从而证出结论;
,从而证出结论;
(2)根据题意,画出图形,延长ED至W,使得DW=DM,连接WM,先证出△WDM是等边三角形,然后利用ASA证出△WMG≌△DMB,从而得出WG=DB,然后利用等量代换即可得出结论;
(3)延长BD至H,使得DH=DN,连接HN,先证出△NDH是等边三角形,然后利用ASA证出△DNG≌△HNB,从而得出DG=HB,然后利用等量代换即可得出结论;
(1)证明:如图1所示:

在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠ABC=60°,BC=![]()
∵BD平分∠ABC,
∴∠1=∠DBA=∠A=30°.
∴DA=DB.
∵DE⊥AB于点E.
∴AE=BE=![]()
∴BC=BE.
∴△EBC是等边三角形;
(2)作图如下,结论:AD=DG+DM.理由如下
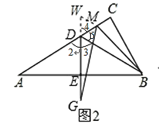
延长ED至W,使得DW=DM,连接WM.
由(1)得DA=DB,∠A=30°.
∵DE⊥AB于点E.
∴∠2=∠3=60°.
∴∠4=∠2=60°,∠5=180°-∠2-∠3=60°
∴△WDM是等边三角形.
∴WD=DM=WM,∠W=∠WMD=60°
∴∠W =∠5.
∴∠WMD+∠DMG=∠BMG+∠DMG
即∠WMG=∠DMB.
在△WMG和△DMB中
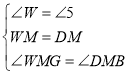
∴△WMG≌△DMB (ASA).
∴WG=DB.
∵WG= DG + WD = DG + DM,
∴DB= DG + DM.
∴AD= DG + DM.
(3)结论:AD=DGDN.
证明:延长BD至H,使得DH=DN,连接HN.
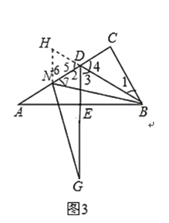
由(1)得DA=DB,∠A=30°.
∵DE⊥AB于点E.
∴∠2=∠3=60°.
∴∠4=∠5=60°
∴△NDH是等边三角形.
∴NH=ND,∠H=∠6=60°
∴∠H=∠2.
∵∠BNG=60°
∴∠BNG+∠7=∠6+∠7
即∠DNG=∠HNB.
在△DNG和△HNB中
∴△DNG≌△HNB(ASA).
∴DG=HB.
∵HB=HD+DB=ND+AD,
∴DG=ND+AD.
∴AD=DGND.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线,且
点的一条直线,且![]() 、
、![]() 在
在![]() 的异侧,
的异侧,![]() 于
于![]() ,
,![]() 于
于![]() .
.
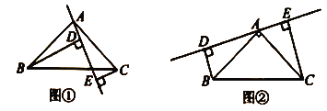
(1)求证:![]() .
.
(2)若将直线![]() 绕点
绕点![]() 旋转到图②的位置时(
旋转到图②的位置时(![]() ),其余条件不变,问
),其余条件不变,问![]() 与
与![]() 、
、![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E、G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=2,连接CF.当△CGF是直角三角形时,线段AE的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
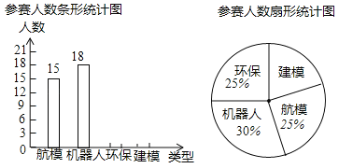
【题目】为了提高科技创新意识,我市某中学在“2018年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:
请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,请用列表或画树状图的方法求选取的两人中恰为1男生1女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)相交于A(1,2),B(n,-1)两点.
(m≠0)相交于A(1,2),B(n,-1)两点.
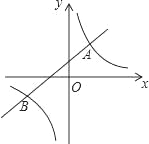
(1)求双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式kx+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形的铁片ABC的两条直角边BC,AC的长分别为3cm和4cm,如图所示分别采用⑴,⑵两种方法,剪去一块正方形铁片,为了使剪去正方形铁片后剩下的边角料较少,试比较哪一种剪法较为合理,并说明理由.
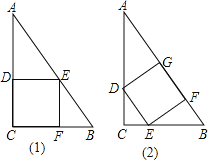
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com