
【题目】如图,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E、G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=2,连接CF.当△CGF是直角三角形时,线段AE的长为______.

【答案】2或6或![]() 或
或![]()
【解析】
由题意得,分∠FGC和∠FCG和∠GFC为直角讨论,①当∠GFC为90![]() 时,E、F、C三点在同一直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解;
时,E、F、C三点在同一直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解;
②当∠GCF=90![]() ,此时F点正好落在BC上, △AEH≌△CGF, △AEH∽△GDH,可求得AE的值;
,此时F点正好落在BC上, △AEH≌△CGF, △AEH∽△GDH,可求得AE的值;
③当∠CGF=90![]() 时,C,G,H共线,所以不可能.
时,C,G,H共线,所以不可能.
解:①由题意得,∠FGC和∠FCG都不能为直角,当∠GFC为90![]() 时,E、F、C三点在同一直线上,所以△AEH∽△BCE,
时,E、F、C三点在同一直线上,所以△AEH∽△BCE,![]()
![]() ,
,
设AE=x,有![]() ,可得x=2或者x=6,
,可得x=2或者x=6,
②当∠GCF=90![]() ,此时F点正好落在BC上,则△AEH≌△CGF, △AEH∽△GDH,则
,此时F点正好落在BC上,则△AEH≌△CGF, △AEH∽△GDH,则
![]() ,解得x=4+2
,解得x=4+2![]() 或x=4-2
或x=4-2![]() ,
,
③当∠CGF=90![]() 时,C,G,H共线,所以不可能;
时,C,G,H共线,所以不可能;
故答案:2或6或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
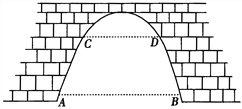
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援困山区,某学校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品与用120元购买A型学习用品的件数相同.
(1)求A,B两种学习用品的单价各是多少元;
(2)若购买A、B两种学习用品共1000件,且总费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
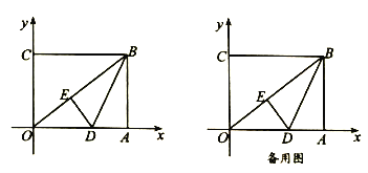
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() .
.
(1)如图![]() ,连接
,连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)点![]() 是线段
是线段![]() 上的一点(不与点
上的一点(不与点![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,请你在图
,请你在图![]() 中画出完整图形,并直接写出
中画出完整图形,并直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究
,试探究![]() 与
与![]() 数量之间的关系,并说明理由.
数量之间的关系,并说明理由.
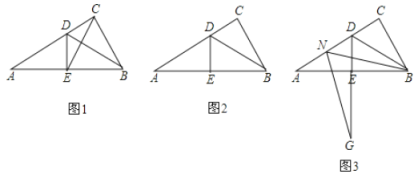
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1) 求y与x的函数关系式;
(2) 根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的![]() ,那么他的月收入最高能达到多少元?
,那么他的月收入最高能达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识链接)连结三角形两边中点的线段,叫做三角形的中位线.
(动手操作)小明同学在探究证明中位线性质定理时,是沿着中位线将三角形剪开然后将它们无缝隙、无重叠的拼在一起构成平行四边形,从而得出:三角形中位线平行于第三边且等于第三边的一半.
(性质证明)小明为证明定理,他想利用三角形全等、平行四边形的性质来证明.请你帮他完成解题过程(要求:画出图形,根据图形写出已知、求证和证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com