
【题目】(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
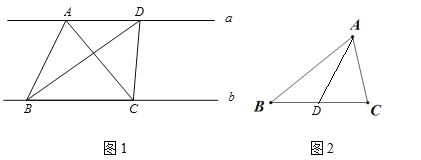

(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则![]() .
.
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组数据:98,99,99,100和98.5,99,99,99.5,则关于以下统计量说法不正确的是( )
A. 平均数相等
B. 中位数相等
C. 众数相等
D. 方差相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,在第一阶段的比赛中,每队都进行了8场比赛,小虎足球队胜了4场,平2场,负2场,得14分;小豹足球队胜了6场,平1场,负1场,得19分.已知,记分规则中,负1场得0分.
(1)求胜1场、平1场各得多少分?
(2)足球联赛结束后,小狮足球队共参加了17场比赛,得了24分,且踢平场数是所胜场数的正整数倍,请你想一想,小狮足球队所负场数有______种可能性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:

(1)图1中“统计与概率”所在扇形的圆心角为 度;
(2)图2、3中的a= ,b= ;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活常识:射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图1,MN是平面镜,若入射光线AO与水平镜面夹角为∠1,反射光线OB与水平镜面夹角为∠2,则∠1=∠2.

(1)现象解释:如图2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.已知:∠1=55°,求∠4的度数.
(2)尝试探究:如图3,有两块平面镜OM,ON,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD相交于点E,若∠MON=46°,求∠CEB的度数.

(3)深入思考:如图4,有两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD,光线AB与CD所在的直线相交于点E,∠BED=β,α与β之间满足的等量关系是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
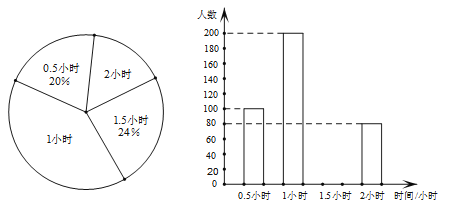
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com