
| 直线条数 | 把平面分成部分数 | 写成和形式 |
| 1 | 2 | 1+1 |
| 2 | 4 | 1+1+2 |
| 3 | 7 | 1+1+2+3 |
| 4 | 11 | 1+1+2+3+4 |
| … | … | … |
分析 (1)根据已知探究的结果可以算出当直线条数为5时,把平面最多分成16部分;
(2)通过已知探究结果,写出一般规律,当直线为n条时,把平面最多分成1+1+2+3+…+n,求和即可.
解答 解:(1)根据已知探究的结果知:
当直线条数为5时,把平面最多分成1+1+2+3+4+5=16部分,
故答案为:16,1+1+2+3+4+5.
(2))通过已知探究结果,
当直线为n条时,
把平面最多分成:1+1+2+3+3+…+n=$\frac{(1+n)n}{2}$+1=$\frac{{n}^{2}+n+2}{2}$.
故答案为:$\frac{{n}^{2}+n+2}{2}$.
点评 题目考查了图形的变化,通过直线分平面探究其中的隐含规律,解决此题关键是写出和的形式,另外,等差数列求和公式应该应用熟练.


科目:初中数学 来源: 题型:选择题
| A. | V=30P | B. | P=V+900 | C. | P=30V | D. | PV=30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
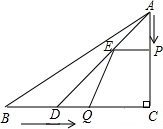 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).当一个点到达终点时,另一个点随之停止运动.
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1厘米/秒的速度沿AC向终点C运动;点Q以1.25厘米/秒的速度沿BC向终点C运动.过点P作PE∥BC交AD于点E,连接EQ.设动点运动时间为t秒(t>0).当一个点到达终点时,另一个点随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
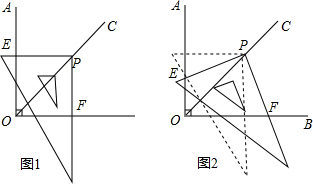
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{{{(-5)}^2}}$=-5 | C. | ±$\sqrt{64}$=±8 | D. | $\root{3}{-27}$=-9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com