
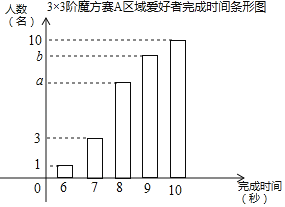
����Ŀ����2017��������21�⣩ij������ħ����������������ع�600��ħ�������߲μӣ����δ������ֽ���3��3��ħ��������ί�������������ƽ���ֵ�20������ÿ������30��ͬʱ���б��������ʱ��С��8��İ����߽�����һ�ֽ�����ͼ��3��3��ħ����A����30�����������ʱ��ͳ��ͼ����
��A����3��3��ħ�������߽�����һ�ֽ���������ı������������������ʾ����
����3��3��ħ��������������������һ�£������A�����ͳ�ƽ��������3��3��ħ�����������һ�ֽ����������
����3��3��ħ����A���������ʱ���ƽ��ֵΪ8.8�룬�����Ŀ�����������ʱ��Ϊ8��İ����ߵĸ��ʣ��������������ʾ����
���𰸡���A��������һ�ֽ������������Ϊ�� ![]() ���ڹ��ƽ�����һ�ֽ��������Ϊ80�ˣ�
���ڹ��ƽ�����һ�ֽ��������Ϊ80�ˣ�
�������ʱ��Ϊ8��İ����ߵĸ���Ϊ![]() ��
��
����������������ͼ֪1��6�룬3��7�룬С��8��İ����߹���4�ˣ�������һ�ֽ������������Ϊ4��30������Ϊ���������������һ�£����Խ�����һ�ֵ�����Ϊ��600��A��������һ�ֽ���������������������ʱ���ƽ��ֵ��A��30�ˣ��õ�����a��b�Ķ�Ԫһ�η����飬���a��b���õ����ʱ��8��İ����ߵĸ��ʣ�
�����������A��С��8��Ĺ���3+1=4���ˣ�
����A��������һ�ֽ������������Ϊ��![]() ��
��
�����ƽ�����һ�ֽ��������Ϊ600��![]() =80���ˣ���
=80���ˣ���
����ΪA���������ʱ���ƽ��ֵΪ8.8�룬
���ԣ�1��6+3��7+a��8+b��9+10��10����30=8.8
����8a+9b=137������1+3+a+b+10=30����a+b=16
����![]() ,���a=7��b=9
,���a=7��b=9
���Ը������ʱ��Ϊ8��İ����ߵĸ���Ϊ![]() ��
��


 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
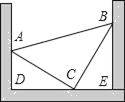
����Ŀ����ͼ����һ�����ֱ�����������(��ABC�����С�ACB��90��)��������һ�����ڣ���������A��B��C�ֱ����ڰ����ڱ��ϣ���֪��ADE����BED��90�㣬���AD��5cm��BE��7cm���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
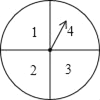
����Ŀ��С����С��������ͼ��ʾ��ת������Ϸ��ת�̵����汻��Ϊ�����ȵ�4�����������ҷֱ��������1��2��3��4����Ϸ�������£����˸�ת��ת��һ�Σ��ֱ��¼ָ��ֹͣʱ����Ӧ�����֣������ε����ֶ�����������С��ʤ�������ε����ֶ���ż������С��ʤ�������ε���������ż����Ϊƽ�֣�����������⣺
��1��С��ת��ת�̣���ת��ָ��ֹͣ����Ӧ��������Ϊ�����ĸ����Ƕ��٣�
��2������Ϸ�Ƿ�ƽ�������б�����״ͼ�ķ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���4x2+4��m��1��x+m2=0
��1����m��ʲô��Χȡֵʱ������������ʵ������
��2���跽��������ʵ����x1 �� x2 �� ��mΪ��ֵʱ��x12+x22=17��
��3��������������ʵ����x1��x2�� ��x1��x2�ܷ�ͬ�ţ�����ͬ�ţ��������Ӧm��ȡֵ��Χ��������ͬ�ţ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
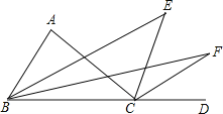
����Ŀ����ͼ���ڡ�ABC�У���A=80������ABC���ACD��ƽ���߽��ڵ�E����EBC���ECD��ƽ�����ཻ�ڵ�F�����BFC=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƕ��κ��� y��ax2��bx��c��a��0����ͼ���һ���֣� ������������ ����a+b+c=0����b��2a����ax2+bx+c=0�������ֱ�Ϊ��3��1����a��2b+c��0��������ȷ��������__________����ֻҪ����д��ȷ�������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪��ƽ��ֱ������ϵxoy�У����κ���y=-2x+bx+c��ͼ����A��-3,0���͵�B��0,6������1����˶��κ����Ľ���ʽ����2����������κ�����ͼ������ƽ��5����λ��Ķ�����ΪC��ֱ��BC��x���ཻ�ڵ�D,����sin��ABD����3���ڵڣ�2��С��������£�����OC����̽��ֱ��AB��OC��λ�ù�ϵ������˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
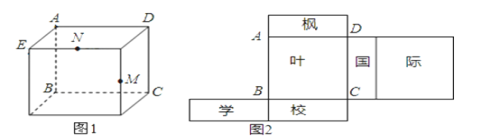
����Ŀ����ͼ��ͼ1Ϊһ�������壬AB=AD=16��AE=6��ͼ2Ϊ��ͼ�ı���չ��ͼ�������Ҫ��ش����⣺
��1������ѧ���Ķ�������ʲô��
��2��ͼ1�У�M��NΪ��������е㣬����ͼ2�л�����M��N��λ�ã� �����ͼ2����ABN�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
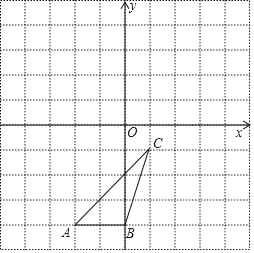
����Ŀ����ͼ����ABC�����������ֱ���A����2����4����B��0����4����C��1����1����
��1����ͼ�л�����ABC����ԭ��ԳƵġ�A1B1C1��
��2����ͼ�л�����ABC��ԭ��O��ʱ����ת90����ġ�A2B2C2��
��3���ڣ�2���������£����A�˶�·������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com