
【题目】 已知在平面直角坐标系xoy中,二次函数y=-2x+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
【答案】(1)y=-2x2-4x+6;(2)sin∠ABD=![]() ;(3)略.
;(3)略.
【解析】
试题(1)把点A、B的坐标代入函数解析式计算求出b、c的值,即可得解;
(2)先求出抛物线的顶点坐标,再根据向右平移横坐标加,求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0),然后利用待定系数法求出直线BC的解析式,再求出与x轴的交点D的坐标,过点A作AH⊥BD于H,先求出OD,再利用勾股定理列式求出BD,然后求出△ADH和△BDO相似,利用相似三角形对应边成比例列式求出AH,再利用勾股定理,然后根据锐角的正弦等于对边比斜边列式计算即可得解;
(3)过点C作CP⊥x轴于P,分别求出∠BAO和∠COP的正切值,根据正切值相等求出∠BAO=∠COP,再根据同位角相等,两直线平行解答.
试题解析:(1)由题意得, 2×93b+c=0 c=6 ,
解得 b=4 c=6 ,
所以,此二次函数的解析式为y=-2x2-4x+6;
(2)∵y=-2x2-4x+6=-2(x+1)2+8,
∴函数y=2x2-4x+6的顶点坐标为(-1,8),
∴向右平移5个单位的后的顶点C(4,8),
设直线BC的解析式为y=kx+b(k≠0),
则![]() ,
,
解得 ,
,
所以,直线BC的解析式为y=![]() x+6,
x+6,
令y=0,则![]() x+6=0,
x+6=0,
解得x=-12,
∴点D的坐标为(-12,0),
过点A作AH⊥BD于H,
OD=12,BD=![]() ,
,
AD=-3-(-12)=-3+12=9,
∵∠ADH=∠BDO,∠AHD=∠BOD=90°,
∴△ADH∽△BDO,
∴AH:OB ="AD:BD" ,
即AH:6 =9:![]() ,
,
解得AH=![]() ,
,
∵AB=![]() ,
,
∴sin∠ABD=![]() ;
;
(3)过点C作CP⊥x轴于P,
由题意得,CP=8,PO=4,AO=3,BO=6,
∴tan∠COP=![]() =2,
=2,
tan∠BAO=![]() =2,
=2,
∴tan∠COP=tan∠BAO,
∴∠BAO=∠COP,
∴AB∥OC.



科目:初中数学 来源: 题型:
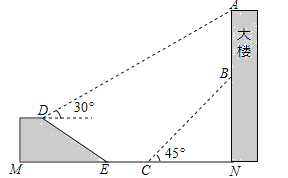
【题目】(12分)如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:![]() (即tan∠DEM=1:
(即tan∠DEM=1:![]() ),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:
),且D、M、E、C、N、B、A在同一平面内,E、C、N在同一条直线上,求条幅的长度(结果精确到1米)(参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(13分)如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.

(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
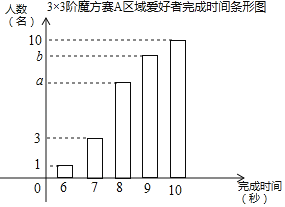
【题目】(2017湖南株洲第21题)某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:
①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).
②若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数.
③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=x2+bx+c 的图象如图所示,它与 x 轴的一个交点坐标为(1,0),与 y轴的交点坐标为(0,-3).
(1)求出 b,c 的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值 y 为正数时,自变量 x 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
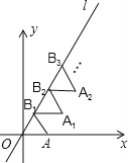
【题目】如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
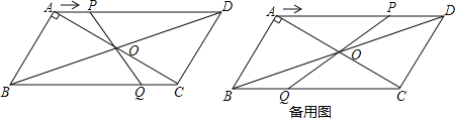
【题目】 如图,在ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动速度为lcm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com