
【题目】已知二次函数 y=x2+bx+c 的图象如图所示,它与 x 轴的一个交点坐标为(1,0),与 y轴的交点坐标为(0,-3).
(1)求出 b,c 的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值 y 为正数时,自变量 x 的取值范围.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
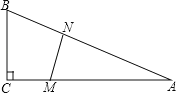
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知在平面直角坐标系xoy中,二次函数y=-2x+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
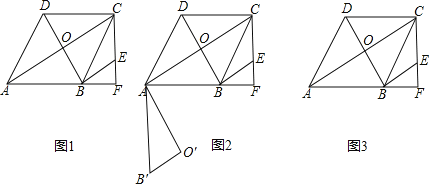
【题目】如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适当路径先运动到O′点,再沿O′A运动至A点,再从A点沿适当的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
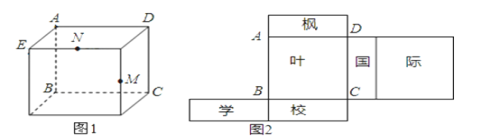
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
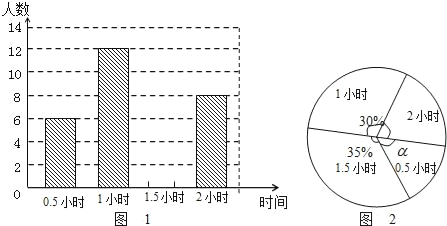
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com