
【题目】如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适当路径先运动到O′点,再沿O′A运动至A点,再从A点沿适当的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
【答案】(1)8;(2)12![]() 12;(3)t=2或2
12;(3)t=2或2![]() 或6s
或6s
【解析】
(1)根据菱形的性质和已知边、已知角,可证得△BCF、△BEF均是一角为30°的直角三角形,继而可求BE的长;
(2)根据菱形的性质,连接CO′交BD于Q,连接AQ,可得Q点的最短路径=QO′+O′A +AP′=CQ+QO′+AO=CO′+AO′,再根据勾股定理即可求解;
(3)①当点B1与F重合时,如图3所示,点O1在BC的中点,△O″FC为等腰三角形,可得t![]() 2s;②如图4所示,当FC=FO″时,△O″FC为等腰三角形,易证四边形HO1B1F是平行四边形,t
2s;②如图4所示,当FC=FO″时,△O″FC为等腰三角形,易证四边形HO1B1F是平行四边形,t![]() 2
2![]() s;③如图5所示,当点A1与F重合时, CF=CO″,△O″FC为等腰三角形,t=6s.
s;③如图5所示,当点A1与F重合时, CF=CO″,△O″FC为等腰三角形,t=6s.
解:(1)如图1中,
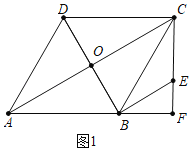
∵四边形ABCD是菱形,∠DAB=60°,
∴AB=BC=8![]() ,∠BAC=∠BCA=30°,
,∠BAC=∠BCA=30°,
∵BC∥AD,BE∥AC,
∴∠CBF=∠DAB=60°,∠BCA=∠CBE=30°,
∵CF⊥BF,
∴∠F=90°,
∴∠BCE=∠EBC=30°,
∴BE=EC,
在Rt△BCF中,BF![]() BC=4
BC=4![]() ,
,
在Rt△BEF中,cos30°![]() ,
,
∴BE=![]() =8.
=8.
(2)如图2中,
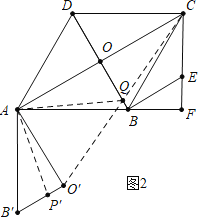
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,
∴A、C关于BD对称,
连接CO′交BD于Q,连接AQ,此时Q点的运动路径最短,
最短路径=QO′+O′A+AP′=CQ+QO′+AO=CO′+AO′![]() 12=12
12=12![]() 12.
12.
(3)①如图3中,当点B1与F重合时,点O1在BC的中点,易知AA1![]() AB=4
AB=4![]() ,
,
∴t![]() 2s.
2s.

②如图4中,当FC=FO″时,设FO″交BC于H,易证四边形HO1B1F是平行四边形,
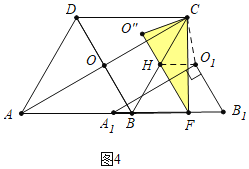
FH![]() BC=4
BC=4![]() ,HO″=HO1=B1F=12﹣4
,HO″=HO1=B1F=12﹣4![]() ,
,
∴AA1=12,t![]() 2
2![]() s.
s.
③如图5,当点A1与F重合时,CF=CO″,此时AA1=12![]() ,t=6s.
,t=6s.
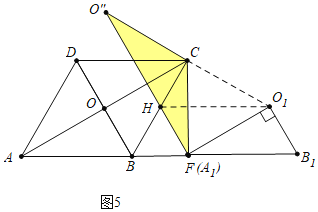
综上所述,当t=2或2![]() 或6s时,△CFO″是等腰三角形.
或6s时,△CFO″是等腰三角形.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
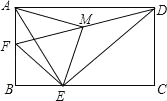
【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A.5 B.2![]() C.2
C.2![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
A | B | C | D | E | 平均分 | 方差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| 2 |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
|
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进同一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果每箱的单价是多少元?
(2)该水果店主计划两批水果的售价均定为每千克4元,每箱10千克,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了2%的损耗,但这两批水果销售完后仍赚了不低于2346元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=x2+bx+c 的图象如图所示,它与 x 轴的一个交点坐标为(1,0),与 y轴的交点坐标为(0,-3).
(1)求出 b,c 的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值 y 为正数时,自变量 x 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
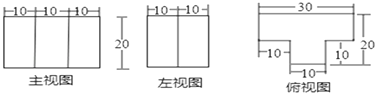
【题目】杭州某零件厂刚接到要铸造5000件铁质工件的订单,下面给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少千克的防锈漆?(铁的密度为7.8g/cm3 ,1千克防锈漆可以涂4m2的铁器面,三视图单位为cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
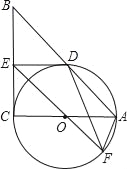
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.在△ABC中,AB=AC,点D为BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,则四边形AEDF的周长等于这个三角形的( )
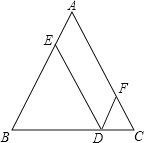
A.周长B.周长的一半
C.两腰长和的一半D.两腰长的和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com