
【题目】某学校有两个校区:南校和北校,这两个校区九年级学生各有300名,为了解这两个校区九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据,从南校和北校两个校区的九年级各随机抽取10名学生,进行英语单词测试,测试成绩(百分制)如下:
南校 92 100 86 89 73 98 54 95 98 85
北校 100 100 94 83 74 86 75 100 73 75
②整理、描述数据,按如下分数段整理、描述这两组样本数据:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
南校 | 1 | 0 | 1 | 3 | 5 |
北校 | 0 | 0 | 4 | 2 | 4 |
(说明:成绩90分及以上为优秀,80~89分分为良好,60~79分为合格,60分以下为不合格)
③分析数据,对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数、方差如下表:
校区 | 平均数 | 中位数 | 众数 | 方差 |
南校 | 87 | 90.5 |
| 179.4 |
北校 | 86 |
|
| 121.6 |
④得出结论.
结合上述统计全过程,回答下列问题:
(1)补全③中的表格.
(2)请估计北校九年级学生英语单词掌握优秀的人数.
(3)你认为哪个校区的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)
【答案】(1)补全表格见解析;(2)估计北校九年级学生英语单词掌握优秀的人数为120人;(3)我认为南校区的九年级学生英语单词掌握得比较好,理由见解析.
【解析】
(1)一组数据中出现次数最多的数据叫做众数,依据已知条件即可补全③中的表格;
(2)依据![]() ×300,即可得到北校九年级学生英语单词掌握优秀的人数;(3)依据每个校区的英语测试的成绩的平均数以及中位线的高低,即可得到哪个校区的九年级学生英语单词掌握得比较好.
×300,即可得到北校九年级学生英语单词掌握优秀的人数;(3)依据每个校区的英语测试的成绩的平均数以及中位线的高低,即可得到哪个校区的九年级学生英语单词掌握得比较好.
(1)由题可得,南校区的九年级随机抽取的10名学生的成绩的众数为98,
北校区的九年级随机抽取的10名学生的成绩为:73、74、75、75、83、86、94、100、100、100,
∴北校区的九年级随机抽取的10名学生的成绩的中位数为:84.5;而众数为100;
故答案为:98,84.5,100;
(2)北校九年级学生英语单词掌握优秀的人数为:![]() ×300=120(人).
×300=120(人).
(3)我认为南校区的九年级学生英语单词掌握得比较好,理由如下:
①南校区的九年级学生在英语单词测试中,平均数较高,表示南校区的九年级学生的英语单词掌握情况较好;
②南校区的九年级学生在英语单词测试中,中位数较高,表示南校区英语单词掌握优秀的学生较多.(答案不唯一)


科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=1:1:2B.a:b:c=3:4:5
C.∠A:∠B:∠C=3:4:5D.a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 为菱形,点
为菱形,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向终点
向终点![]() 运动,连接
运动,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当动点
,当动点![]() 运动了
运动了![]() 秒时.
秒时.
(1)![]() 点的坐标为________,
点的坐标为________,![]() 点的坐标为________(用含
点的坐标为________(用含![]() 的代数式表示);
的代数式表示);
(2)记![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式
的函数关系式![]() ,并求出当
,并求出当![]() 取何值时,
取何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
(2)在![]() 出发的同时,有一动点
出发的同时,有一动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,试求当
移动,试求当![]() 为何值时,
为何值时,![]() 与
与![]() 相似.
相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:在路上,我们经常看到这样的汽车牌照号:“辽A30803”,“辽P12321”,“京C76H67”,…,给人以对称美的感受.除了表示地区标志的汉字和字母(如:沈阳车牌辽A,葫芦岛车牌辽P等)以外,像“30803”、“76H67”这样的由数或由数和字母共同组成的车牌号,我们称之为“轴对称车牌号”.在正整数中,现定义为,“形如![]() 的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
的正整数叫做轴对称数.”比如:99,363,2112等都是轴对称数.
(1)写出最小的五位“轴对称数”;
(2)请你设计一个我们葫芦岛市的车牌号,要求:此车牌号的后五位是“轴对称车牌号”,且由数字和字母组成的;
(3)已知某车的车牌号是由数字组成的“轴对称车牌号”,设首位数字为m,去掉首尾数字后的中间的三位数为n.已知多项式x2﹣2m能用公式法分解因式,![]() n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
n是多项式a﹣1与多项式a+102相乘得到的多项式的一次项系数,求出符合条件的车牌号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,在四边形ABCD中,∠A=∠C=90°,AD=CD,点E、F分别在边AB、BC上,ED=FD,证明:∠ADE=∠CDF.
(拓展)如图②,在菱形ABCD中,∠A=120°,点E、F分别在边AB、BC上,ED=FD.若∠EDF=30°,求∠CDF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路列车(简称:高铁)是人们出行的重要交通工具:已知高铁平均速度是普通铁路列车(简称:普客)平均速度的的3倍.同样行驶690km,高铁比普客少用4.6h.
(1)求高铁的平均速度.
(2)某天王老师乘坐8:40出发的高铁,到里程1050km的A市参加当天14:00召开的会议.若他从A市高铁站到会议地点最多还需要1.5h,试问在高铁准点到达的情况下,他能在开会之前赶到会议地点吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
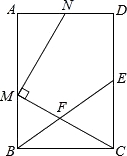
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE.
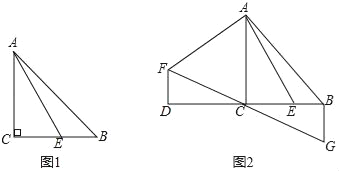
(1)如图1,当∠BAE=15°,CE=![]() 时,求AB的长.
时,求AB的长.
(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com