
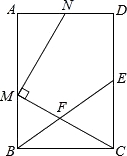
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
【答案】(1)详见解析;(2)3;(3)n=4.
【解析】
试题分析:(1)如图1,易证△BMF≌△ECF,则有BM=EC,然后根据E为CD的中点及AB=DC就可得到AM=EC;(2)如图2,设MB=a,易证△ECF∽△BMF,根据相似三角形的性质可得EC=2a,由此可得AB=4a,AM=3a,BC=AD=2a.易证△AMN∽△BCM,根据相似三角形的性质即可得到AN=![]() a,从而可得ND=AD﹣AN=
a,从而可得ND=AD﹣AN=![]() a,就可求出
a,就可求出![]() 的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
的值;(3)如图3,设MB=a,同(2)可得BC=2a,CE=na.由MN∥BE,MN⊥MC可得∠EFC=∠HMC=90°,从而可证到△MBC∽△BCE,然后根据相似三角形的性质即可求出n的值.
试题解析:(1)当F为BE中点时,如图1,
则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
 ,
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=![]() DC,
DC,
∴BM=EC=![]() DC=
DC=![]() AB,
AB,
∴AM=BM=EC;
(2)如图2,
设MB=a,
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴![]() =2,
=2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵![]() =2,
=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() a,ND=AD﹣AN=2a﹣
a,ND=AD﹣AN=2a﹣![]() a=
a=![]() a,
a,
∴ =3;
=3;
(3)当![]() =n时,如图3,
=n时,如图3,
设MB=a,同(2)可得BC=2a,CE=na.
∵MN∥BE,MN⊥MC,
∴∠EFC=∠HMC=90°,
∴∠FCB+∠FBC=90°.
∵∠MBC=90°,
∴∠BMC+∠FCB=90°,
∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,
∴△MBC∽△BCE,
∴![]() ,
,
∴![]() ,
,
∴n=4.





科目:初中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() 有增根,则
有增根,则![]() 的值为__________.
的值为__________.
【答案】2
【解析】方程两边都乘(x2),得
x+x2=a,即a=2x2.
分式方程的增根是x=2,
∵原方程增根为x=2,
∴把x=2代入整式方程,得a=2,
故答案为:2.
点睛:本题考查了分式方程的增根,增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出a的值.
【题型】填空题
【结束】
17
【题目】反比例函数y=![]() 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校有两个校区:南校和北校,这两个校区九年级学生各有300名,为了解这两个校区九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据,从南校和北校两个校区的九年级各随机抽取10名学生,进行英语单词测试,测试成绩(百分制)如下:
南校 92 100 86 89 73 98 54 95 98 85
北校 100 100 94 83 74 86 75 100 73 75
②整理、描述数据,按如下分数段整理、描述这两组样本数据:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
南校 | 1 | 0 | 1 | 3 | 5 |
北校 | 0 | 0 | 4 | 2 | 4 |
(说明:成绩90分及以上为优秀,80~89分分为良好,60~79分为合格,60分以下为不合格)
③分析数据,对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数、方差如下表:
校区 | 平均数 | 中位数 | 众数 | 方差 |
南校 | 87 | 90.5 |
| 179.4 |
北校 | 86 |
|
| 121.6 |
④得出结论.
结合上述统计全过程,回答下列问题:
(1)补全③中的表格.
(2)请估计北校九年级学生英语单词掌握优秀的人数.
(3)你认为哪个校区的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
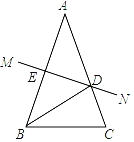
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;
(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在150≤x<175范围内,随机抽取初一学生进行抽样调查.抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:

身高情况分组表
组别 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高在155≤x<165之间的学生有18人;
②初一学生中女生的身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④初一学生身高在160≤x<170之间的学生约有800人.
其中合理的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年女排世界杯中,中国女排以11站全胜且只丢3局的成绩成功卫冕本届世界杯冠军.某校七年级为了弘扬女排精神,组建了排球社团,通过测量同学们的身高(单位:cm),并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.

(1)填空:样本容量为___,a=___;
(2)把频数分布直方图补充完整;
(3)若从该组随机抽取1名学生,估计这名学生身高低于165cm的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再解决问题.
阅读:材料一配方法可用来解一元二次方程.例如,对于方程![]() 可先配方
可先配方![]() ,然后再利用直接开平方法求解方程.其实,配方还可以用它来解决很多问题.
,然后再利用直接开平方法求解方程.其实,配方还可以用它来解决很多问题.
材料二对于代数式![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 有最小值
有最小值![]() ,且当
,且当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
类似地,对于代数式![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 有最大值
有最大值![]() ,且当
,且当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
解答下列问题:
![]() 填空:①当
填空:①当![]() ________时,代数式
________时,代数式![]() 有最小值为________;
有最小值为________;
②当![]() ________时,代数式
________时,代数式![]() 有最大值为________.
有最大值为________.
![]() 试求代数式
试求代数式![]() 的最小值,并求出代数式取得最小值时的
的最小值,并求出代数式取得最小值时的![]() 的值.
的值.
(要求写出必要的运算推理过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com