
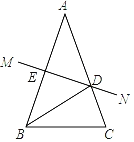
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
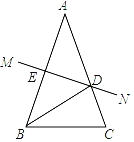
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
【答案】(1)30°;(2)32.
【解析】
(1)由在△ABC中,AB=AC,∠A=40°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D.根据线段垂直平分线的性质,可得AD=BD,可得∠ABD的度数,即可求得∠DBC的度数.
(2)由△CBD的周长为20,可得AC+BC=20,根据AB=2AE=12,即可得出答案.
解:(1)解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°.
(2)∵MN垂直平分AB,
∴DA=DB,AB=2AE=12,
∵BC+BD+DC=20,
∴AD+DC+BC=20,
∴AC+BC=20,
∴△ABC的周长为:AB+AC+BC=12+20=32.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是直线
是直线![]() 两侧的点,以
两侧的点,以![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于
于![]() ,
,![]() 两点,又分别以
两点,又分别以![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点D,连接
的长为半径画弧,两弧交于点D,连接![]() ,
,![]() ,
,![]() 下列结论不一定正确的是( )
下列结论不一定正确的是( )

A.![]() B.点
B.点![]() ,
,![]() 关于直线
关于直线![]() 对称
对称
C.点![]() ,
,![]() 关于直线
关于直线![]() 对称D.
对称D.![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 为菱形,点
为菱形,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向终点
向终点![]() 运动,连接
运动,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当动点
,当动点![]() 运动了
运动了![]() 秒时.
秒时.
(1)![]() 点的坐标为________,
点的坐标为________,![]() 点的坐标为________(用含
点的坐标为________(用含![]() 的代数式表示);
的代数式表示);
(2)记![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式
的函数关系式![]() ,并求出当
,并求出当![]() 取何值时,
取何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
(2)在![]() 出发的同时,有一动点
出发的同时,有一动点![]() 从
从![]() 点开始在线段
点开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,试求当
移动,试求当![]() 为何值时,
为何值时,![]() 与
与![]() 相似.
相似.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,在四边形ABCD中,∠A=∠C=90°,AD=CD,点E、F分别在边AB、BC上,ED=FD,证明:∠ADE=∠CDF.
(拓展)如图②,在菱形ABCD中,∠A=120°,点E、F分别在边AB、BC上,ED=FD.若∠EDF=30°,求∠CDF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速铁路列车(简称:高铁)是人们出行的重要交通工具:已知高铁平均速度是普通铁路列车(简称:普客)平均速度的的3倍.同样行驶690km,高铁比普客少用4.6h.
(1)求高铁的平均速度.
(2)某天王老师乘坐8:40出发的高铁,到里程1050km的A市参加当天14:00召开的会议.若他从A市高铁站到会议地点最多还需要1.5h,试问在高铁准点到达的情况下,他能在开会之前赶到会议地点吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
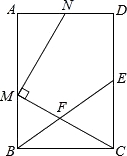
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家主管部门规定:从2008年6月1日起,各商家禁止向消费者免费提供一次性塑料购物袋.为了了解巴中市市民对此规定的看法,对本市年龄在16—65岁之间的居民,进行了400个随机访问抽样调查,并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图.

根据上图提供的信息回答下列问题:
(1)被调查的居民中,人数最多的年龄段是 岁.
(2)已知被调查的400人中有83%的人对此规定表示支持,请你求出31—40岁年龄段的满意人数,并补全图b.
(3)比较21—30岁和41—50岁这两个年龄段对此规定的支持率的高低(四舍五入到1%,注:某年龄段的支持率![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com