
【题目】将纸片△ABC沿DE折叠使点A落在点A’处.
(感知)如图①,点A’落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是 .
(探究)如图②,若A’点落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由?
(拓展)如图③,点A’落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为 度.

【答案】感知:2∠A=∠1 ;探究:2∠A=∠1+∠2,理由详见解析;拓展:28.
【解析】
感知: 运用折叠原理及三角形的外角性质即可解决问题;
探究: 运用折叠原理及四边形的内角和定理即可解决问题;
拓展: 运用三角形的外角性质即可解决问题.
感知:2∠A=2∠1,
理由:如图①:
∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°-∠A,
∠1+∠2=180°+180°-2(∠AED+∠ADE),
∴∠1+∠2=360°-2(180°-∠A)=2∠A;
探究: 2∠A=∠1+∠2.
理由如下:如图②:
∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
拓展:
如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1-∠2=56°,
解得∠A=28°.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店计划购进![]() ,
,![]() 两种型号的电机,其中每台
两种型号的电机,其中每台![]() 型电机的进价比
型电机的进价比![]() 型多
型多![]() 元,且用
元,且用![]() 元购进
元购进![]() 型电机的数量与用
型电机的数量与用![]() 元购进
元购进![]() 型电机的数量相等.
型电机的数量相等.
(1)求![]() ,
,![]() 两种型号电机的进价;
两种型号电机的进价;
(2)该商店打算用不超过![]() 元的资金购进
元的资金购进![]() ,
,![]() 两种型号的电机共
两种型号的电机共![]() 台,至少需要购进多少台
台,至少需要购进多少台![]() 型电机?
型电机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=![]() (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(1)一次函数和反比例函数的解析式;
(2)求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.

(1)将△PAB绕点B顺时针旋转90°得到△P′CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=![]() ,PB=2
,PB=2![]() ,∠APB=135°,求PC的长.
,∠APB=135°,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读可以增进人们的知识,也能陶冶人们的情操.我们要多阅读有营养的书.某校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 | 阅读时间x(h) | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | b |
D | 30≤x<40 | 140 |
E | x≥40 | c |

请结合以上信息解答下列问题:
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, ![]() ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵![]()
∴b=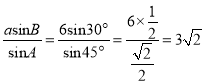 .
.
理解应用:
如图,甲船以每小时30![]() 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10![]() 海里.
海里.
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),直线l1:y=kx+b经过点A、B,OA=OB=3,直线12:y=![]() x﹣2交y轴于点C,且与直线l1交于点D,连接OD.
x﹣2交y轴于点C,且与直线l1交于点D,连接OD.

(1)求直线11的表达式;
(2)求△OCD的面积;
(3)如图(b),点P是直线11上的一动点;连接CP交线段OD于点E,当△COE与△DEP的面积相等时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com