
【题目】如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=![]() (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(1)一次函数和反比例函数的解析式;
(2)求△ACD的面积.

【答案】(1)一次函数的解析式为y=x+1.反比例函数的解析式为y=![]() (2)2
(2)2
【解析】试题分析:(1)根据OA=OB=OD=1,和各坐标轴上的点的特点易得到点A. B.D的坐标,将A. B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,由C点在一次函数的图象上可确定C点坐标,再将C点坐标代入![]() 可确定反比例函数的解析式.
可确定反比例函数的解析式.
(2)根据A(1,0),C(1,2),D(1,0),即可得到![]() 进而得出
进而得出![]() 的面积.
的面积.
试题解析:(1)∵OA=OB=OD=1,
∴点A. B.D的坐标分别为A(1,0),B(0,1),D(1,0),
∵点A.B在一次函数y=kx+b(k≠0)的图象上,
∴![]() 解得
解得![]()
∴一次函数的解析式为y=x+1.
把x=1代入y=x+1得,y=2,
即点C的坐标是(1,2),
又∵点C在反比例函数![]() 的图象上,
的图象上,
∴m=2,
∴反比例函数的解析式为y=2x.
(2)∵CD垂直于x轴,A(1,0),C(1,2),D(1,0),
∴AD=2,CD=2,
∴△ACD的面积为: ![]()


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
已知:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD.
试说明:∠EGF=90°.

解:因为HG∥AB(已知),
所以∠1=∠3( ).
又因为HG∥CD(已知),
所以∠2=∠4( ).
因为AB∥CD(已知),
所以∠BEF+ =180°( ).
又因为EG平分∠BEF(已知),
所以∠1=![]() ∠ ( ).
∠ ( ).
又因为FG平分∠EFD(已知),
所以∠2=![]() ∠ ( ),
∠ ( ),
所以∠1+∠2=![]() ( + ).
( + ).
所以∠1+∠2=90°.
所以∠3+∠4=90°( ),即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将纸片△ABC沿DE折叠使点A落在点A’处.
(感知)如图①,点A’落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是 .
(探究)如图②,若A’点落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由?
(拓展)如图③,点A’落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
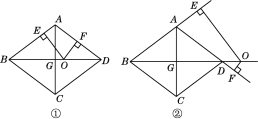
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com