
 如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )
如图,四边形ABCD是正方形,对角线AC,BD交于点O,下列结论:①OA=OB;②∠ACB=45°;③AC⊥BD;④正方形ABCD有四条对称轴.上述结论正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
分析 由正方形的各种性质①正方形的四条边都相等,四个角都是直角;②正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角; ③正方形具有四边形、平行四边形、矩形、菱形的一切性质 ④两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴,逐项分析即可.
解答 解:∵四边形ABCD是正方形,
∴AO=CO=BO=DO,AC⊥BD,
∴∠ACB=45°,故选项①②③正确;
∵AD=BC=CD=AD,AD∥BC,AB∥DC,
∴正方形ABCD有四条对称轴,故选项④正确,
故选A.
点评 本题考查了正方形的性质,正确掌握并且能够灵活运用正方形的各种性质是解题关键.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
 如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.
如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中,AB∥CD,AB=CD,E、F是对角线BD上的两点,如果再添加一个条件,使△ABE≌△CDF,则添加的条件不能是( )
如图,四边形ABCD中,AB∥CD,AB=CD,E、F是对角线BD上的两点,如果再添加一个条件,使△ABE≌△CDF,则添加的条件不能是( )| A. | AE=CF | B. | BE=FD | C. | BF=DE | D. | ∠1=∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
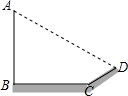 如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )
如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )| A. | (14+2$\sqrt{3}$)米 | B. | 28米 | C. | (7+$\sqrt{3}$)米 | D. | 9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,a,b为数轴上的两点表示的有理数,在a+b,a-b,b-a,ab,|a-b|,|b|-|a|中负数的个数有( )
如图,a,b为数轴上的两点表示的有理数,在a+b,a-b,b-a,ab,|a-b|,|b|-|a|中负数的个数有( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①abc>0;②4a-2b+c>0;③2a-b>0;④a>-1;⑤b2+8a>4ac.其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①abc>0;②4a-2b+c>0;③2a-b>0;④a>-1;⑤b2+8a>4ac.其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com