
【题目】已知:△ABC内接于⊙0,连接AO并延长交BC于点D.

(l)如图l,求证:∠ABC+∠CAD=90°;
(2)如图2,过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE;
(3)如图3,在(2)的条件下,连接BO交DE于点F,延长ED交⊙0于点G,连接AG,若AC=![]() ,BF=OD,求线段AG的长.
,BF=OD,求线段AG的长.
【答案】(1)证明见解析;(2)证明见解析;(3)线段AG的长为![]()
【解析】试题分析:(1)延长AD交⊙O于点M,连接MC,由AM为⊙O的直径得∠ACM=90°,所以∠AMC+∠MAC=90°,根据∠ABC和∠AMC是同弧的所对的角,则有∠ABC=∠AMC,从而得到∠B+∠CAD=90°;(2)过点O作OH⊥AC于H,连接BO,由![]() =
=![]() 得到∠AOB=2∠ACB,又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,∠BOD=∠BDO ,BD=BO 又因为∠BED=∠AHO 、∠ABD=∠AOH,所以△BDE≌△AOH,所以DE=AH ,又因为OH⊥AC ,AH=CH=
得到∠AOB=2∠ACB,又因为∠ADC=2∠ACB,所以∠AOB=∠ADC,∠BOD=∠BDO ,BD=BO 又因为∠BED=∠AHO 、∠ABD=∠AOH,所以△BDE≌△AOH,所以DE=AH ,又因为OH⊥AC ,AH=CH=![]() AC ,所以AC=2DE ;(3)过点O作ON⊥EG于N, OT⊥AB于T连接OG, 因为
AC ,所以AC=2DE ;(3)过点O作ON⊥EG于N, OT⊥AB于T连接OG, 因为![]() ,所以DE=
,所以DE=![]() ,又因为OA=OB,所以∠ABO=∠BAO,因为∠ABO+∠BFE=90° ∠BAO+∠ADE=90°,所以∠BFE=∠OFD=∠ODF ,所以OF=OD ,因为BF=OD ,所以OF=OD=BF,所以△BFE≌△OFN ,所以BE=ON EF=FN,又因为OF=OD ON⊥FD,所以EF=FN=ND=
,又因为OA=OB,所以∠ABO=∠BAO,因为∠ABO+∠BFE=90° ∠BAO+∠ADE=90°,所以∠BFE=∠OFD=∠ODF ,所以OF=OD ,因为BF=OD ,所以OF=OD=BF,所以△BFE≌△OFN ,所以BE=ON EF=FN,又因为OF=OD ON⊥FD,所以EF=FN=ND=![]() ,因为BE=ON OG=BD ,所以△BED≌△NOG,所以ED=NG ,所以EG=
,因为BE=ON OG=BD ,所以△BED≌△NOG,所以ED=NG ,所以EG= ![]() ,又因为ON⊥EG OT⊥AB DE⊥AB ,所以四边形ONET为矩形 ,所以BE=ET=ON,因为OT⊥AB ,所以AT=BT AE=3BE,设AO=BD=r OD=
,又因为ON⊥EG OT⊥AB DE⊥AB ,所以四边形ONET为矩形 ,所以BE=ET=ON,因为OT⊥AB ,所以AT=BT AE=3BE,设AO=BD=r OD=![]() r AD=
r AD=![]() r,因为在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2,则可求出AE=15 ,在△AEG中由勾股定理得AG=
r,因为在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2,则可求出AE=15 ,在△AEG中由勾股定理得AG=![]()
![]()
 或r=-
或r=-![]() (舍去) AE=15 ,在△AEG中由勾股定理得AG=
(舍去) AE=15 ,在△AEG中由勾股定理得AG=![]()
试题解析:
(1)证明:延长AD交⊙O于点M,连接MC,如图所示:

∵AM为⊙O的直径,
∴∠ACM=90°
∴∠AMC+∠MAC=90°
∵![]() =
=![]()
∴∠ABC=∠AMC
∵∠AMC+∠MAC=90° (已证)
∴∠B+∠CAD=90°。
(2) 证明:过点O作OH⊥AC于H,连接BO,如图所示:

∵![]() =
=![]()
∴∠AOB=2∠ACB
∵∠ADC=2∠ACB
∴∠AOB=∠ADC
∴∠BOD=∠BDO
∴BD=BO
∵∠BED=∠AHO ∠ABD=∠AOH
∴△BDE≌△AOH
∴DE=AH
∵OH⊥AC
∴AH=CH=![]() AC
AC
∴AC=2DE
(3) 证明:过点O作ON⊥EG于N, OT⊥AB于T连接OG,如图所示:

∵![]()
∴DE=![]()
∵OA=OB
∴∠ABO=∠BAO
∵∠ABO+∠BFE=90° ∠BAO+∠ADE=90°
∴∠BFE=∠OFD=∠ODF
∴OF=OD
∵BF=OD
∴OF=OD=BF
∴△BFE≌△OFN
∴BE=ON EF=FN
∵OF=OD ON⊥FD
∴EF=FN=ND=![]()
∵BE=ON OG=BD
∴△BED≌△NOG
∴ED=NG
∴EG= ![]()
∵ON⊥EG OT⊥AB DE⊥AB
∴四边形ONET为矩形
∴BE=ET=ON
∵OT⊥AB
∴AT=BT AE=3BE
设AO=BD=r OD=![]() r AD=
r AD=![]() r
r
在Rt△AED中 AE2=AD2-ED2 在Rt△BED中 BE2=BD2-ED2
即![]()

![]() 或r=-
或r=-![]() (舍去) AE=15
(舍去) AE=15
在△AEG中由勾股定理得AG=![]()


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户2014年承包荒山若干亩,改造后,种果树2000棵,总投资7800元,2015年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用含a、b表示两种方式出售水果的收入;
(2)若a=1.3,b=1.1,且两种出售水果方式都在相同时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1 , ∠ABD1与∠ACD1的角平分线交于点D2 , 依此类推,∠ABD4与∠ACD4的角平分线交于点D5 , 则∠BD5C的度数是( ) 
A.56°
B.60°
C.68°
D.94°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图形是由边长为1的正方形按照某种规律排列而组成的.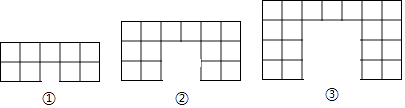
(1)观察图形,填写下表:
图形个数(n) | ① | ② | ③ |
正方形的个数 | 9 | ||
图形的周长 | 16 |
(2)推测第n个图形中,正方形的个数为 , 周长为(都用含n的代数式表示).
(3)写出第2016个图形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)化简:2x2﹣[ ![]() (xy﹣x2)+8xy]﹣
(xy﹣x2)+8xy]﹣ ![]() xy
xy
(2)化简并求值: ![]() x﹣2(x﹣
x﹣2(x﹣ ![]() y2)+(﹣
y2)+(﹣ ![]() x+
x+ ![]() y2),其中:x=﹣1,y=
y2),其中:x=﹣1,y= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( ) 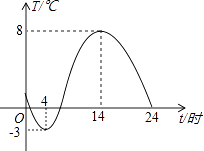
A.凌晨4时气温最低为﹣3℃
B.从0时至14时,气温随时间增长而上升
C.14时气温最高为8℃
D.从14时至24时,气温随时间增长而下降
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com