
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠ABC的平分线BE交⊙O于点E,∠ACB的平分线CF交⊙O于点F,BE和CF相交于点D,四边形AFDE是菱形吗?请证明你的结论.

【答案】四边形AFDE是菱形.证明见解析.
【解析】试题分析:由AB=AC,BE平分∠ABC,CF平分∠ACB,可证∠ABE=∠EBC=∠ACF=∠FCB,再由圆周角定理的推论可证∠FAB=∠ABE=∠EAC=∠ACF.从而可证四边形AFDE是平行四边形,再证AF=AE,即证四边形AFDE是菱形.
解:四边形AFDE是菱形.
证明:∵AB=AC,
∴∠ABC=∠ACB.
又∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠EBC=∠ACF=∠FCB.
∵∠FAB,∠FCB是同弧所对的圆周角,
∴∠FAB=∠FCB,
同理∠EAC=∠EBC.
∴∠FAB=∠ABE=∠EAC=∠ACF.
∴AF∥ED,AE∥FD,
∴四边形AFDE是平行四边形.
∵∠ABE=∠ACF,
∴![]() =
=![]() ,
,
∴AF=AE.
∴四边形AFDE是菱形.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
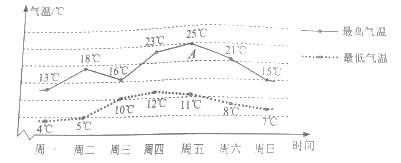
【题目】研究表明,温度对生猪词养有一定的影响.下图是某生猪饲养场查阅的下周天气预报情况,根据图中信息回答下列问题:
(1)周二的最高气温与最低气温分别是多少?
(2)图中点A表示的实际意义是什么?
(3)当一天内的温差超过12C时,生猪可能出现生理异常.为了预防生猪生理异常,养殖场需要在哪几天进行人工调节温度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示, P 是直线 l 外一点,点 A、B、C 在 l 上,且 PB l ,下列说法:① PA、PB、PC 这 3 条线段中, PB 最短;②点 P 到直线 l 的距离是线段 PB 的长;③线段 AB 的长是点 A 到 PB 的距离;④线段 PA 的长是点 P 到直线 l 的距离. 其中正确的是( )
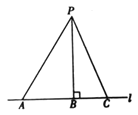
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
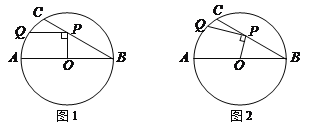
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足![]() +|b﹣3|=0.
+|b﹣3|=0.
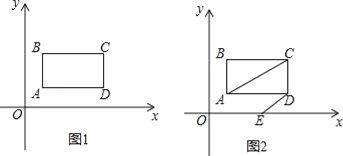
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com