
【题目】已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α= ,β= .
②若∠BAC=54°,∠DAE=36°,则α= ,β= .
③写出α与β的数量关系,并说明理由;

(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.

【答案】(1)①α=12°,β=6°;②α=18°,β=9°,③α=2β,理由见解析;(2)α=2β-180°
【解析】试题分析:(1)①先根据角的和与差求α的值,根据等腰三角形的两个底角相等及顶角为30°得:∠ADE=∠AED=75°,同理可得:∠ACB=∠B=69°,根据外角性质列式:75°+β=69°+12°,可得β的度数;
②同理可求得:α=54°﹣36°=18°,β=9°;
③设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,分别求出∠ADE和∠B,根据∠ADC=∠B+α列式,可得结论;
(2)α=2β﹣180°,理由是:如图(2),设∠E=x°,则∠DAC=2x°,根据∠ADC=∠B+∠BAD,列式可得结论.
解:(1)①∵∠DAE=30°,
∴∠ADE+∠AED=150°,
∴∠ADE=∠AED=75°,
∵∠BAC=42°,
∴α=42°﹣30°=12°,
∴∠ACB=∠B=![]() =69°,
=69°,
∵∠ADC=∠B+α,
∴75°+β=69°+12°,
β=6°;
故答案为:12°,6°;
②∵∠DAE=36°,
∴∠ADE+∠AED=144°,
∴∠ADE=∠AED=72°,
∵∠BAC=54°,
∴α=54°﹣36°=18°,
∴∠ACB=∠B=![]() =63°,
=63°,
∵∠ADC=∠B+α,
∴72°+β=63°+18°,
β=9°;
故答案为:18°,9°;
③α=2β,理由是:
如图(1),设∠BAC=x°,∠DAE=y°,则α=x°﹣y°,
∵∠ACB=∠ABC,
∴∠ACB=![]() ,
,
∵∠ADE=∠AED,
∴∠AED=![]() ,
,
∴β+∠ADE=α+∠ABC,
β+![]() =α+
=α+![]() ,
,
∴α=2β;
(2)α=2β﹣180°,理由是:
如图(2),设∠E=x°,则∠DAC=2x°,
∴∠BAC=∠BAD+∠DAC=α+2x°,
∴∠B=∠ACB=![]() ,
,
∵∠ADC=∠B+∠BAD,
∴β﹣x°=![]() +α,
+α,
∴α=2β﹣180°.


科目:初中数学 来源: 题型:
【题目】探索性问题:
已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0,请回答问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= ;
(2)数轴上a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用t的关系式表示);
②请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF//BC交DC的延长线于点F,连接AF并延长BC的延长线于点G 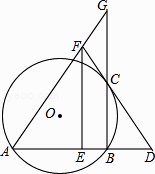
(1)求证:FC=FG;
(2)若BC=4,CG=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧 ![]() 于点D,连接CD、OD.下列结论:①AC∥OD;②CE=OE;③∠OED=∠AOD;④CD=DE.其中正确结论的个数有( )
于点D,连接CD、OD.下列结论:①AC∥OD;②CE=OE;③∠OED=∠AOD;④CD=DE.其中正确结论的个数有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
(1)a+b= ,![]() = ;
= ;
(2)判断b+c,a﹣c,(b+c)(a﹣b)的符号;
(3)判断![]() 的符号.
的符号.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的商品市场指导价为每千克150元,公司的实际销售价格可以浮动x个百分点(即销售价格=150(1+x%)),经过市场调研发现,这种商品的日销售量p(千克)与销售价格浮动的百分点x之间的函数关系为p=﹣2x+24.若该公司按浮动﹣12个百分点的价格出售,每件商品仍可获利10%.
(1)求该公司生产销售每千克商品的成本为多少元?
(2)当该公司的商品定价为多少元时,日销售利润为576元?(说明:日销售利润=(销售价格一成本)×日销售量)
(3)该公司决定每销售一千克商品就捐赠a元利润(a≥1)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于﹣1时,扣除捐赠后的日销售利润随x的增大而减小,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( ) 
A.58
B.59
C.61
D.62
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com