Question

【题目】如图，正方形ABCD中，点E、F分别在AD、CD上，且AE=DF，连接BE、AF，相交于G．求证：AF⊥BE．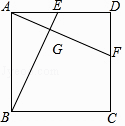

Answer 1

【答案】证明：在正方形ABCD中，AB=AD，∠BAE=∠D=90°， 在△ABE和△ADF中，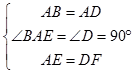
，
∴△ABE≌△ADF（SAS），
∴∠ABE=∠DAF，
∵∠ABE+∠AEG=90°，
∴∠DAF+∠AEG=90°，
∴∠AGE=90°，
∴BE⊥AF．

【解析】根据正方形的四条边都相等可得AB=AD，每一个角都是直角可得∠BAE=∠D=90°，然后利用“边角边”证明△ABE和△ADF全等，由此即可证明．
【考点精析】通过灵活运用正方形的性质，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题．