
【题目】2014年5月30日,云南盈江发生6.1级地震.接到灾情报告后,某武警部队迅速组织了两个救援中队赶赴灾区救援.第一中队有x人,第二中队的人数比第一中队的![]() 少30人.
少30人.
(1)两个中队共有多少人?
(2)由于第一中队任务较重,指挥部决定临时从第二中队调出10人到第一中队,则调动后第一中队的人数比第二中队多多少人?
【答案】(1)两个中队共有![]() 人;
人;
(2)调动后第一中队的人数比第二中队多![]() 人.
人.
【解析】试题分析:(1)用x表示出第一中队的人数,再把两式相加即可;
(2)先用x表示出第一二中队的人数,再把两式相加即可.
试题解析:(1)∵第一中队有x人,第二中队比第一中队人数的![]() 少30人,
少30人,
∴第二中队的人数是(![]() x-30)人,
x-30)人,
∴两个中队共有x+(![]() x-30)=x+
x-30)=x+![]() x-30=(
x-30=(![]() x-30)(人).
x-30)(人).
答:两个中队共有![]() x-30(人);
x-30(人);
(2)∵从第二中队调出10人到第一中队,
∴调动后第一中队的人数是(x+10)人,第二中队的人数是(![]() x-40)人,
x-40)人,
∴(x+10)-(![]() x-40)=x+10-
x-40)=x+10-![]() x+40=(
x+40=(![]() x+50)(人).
x+50)(人).
答:调动后第一中队的人数比第二中队多(![]() x+50)人.
x+50)人.


科目:初中数学 来源: 题型:
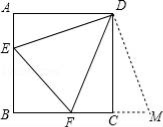
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
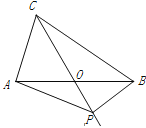
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:如图①,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角:(1)角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
(2)若角的两边分别交AB、CA的延长线于M、N两点,连接MN。在图②中画出图形,再直接写出线段BM、MN、NC之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
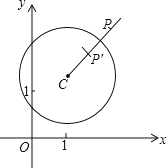
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1,![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
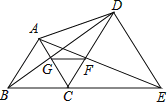
【题目】如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形,其中线段BD交AC于点G,线段AE交CD于点F,求证:
(1)△ACE≌△BCD; (2)![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林从天台柑桔场以2元/kg的成本价购进1000kg的柑桔,在销售过程中有10%的柑桔会损坏不能出售,如果小林想要获得520元的利润,则出售柑桔时,每千克柑桔定价为( )
A. 2.8元 B. 2.7元 C. 2.6元 D. 2.5元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com