[题目]某校把学生的纸笔测试.实践能力.成长记录三项成绩分别按50%.20%.30%的比例计入学期总评成绩.90分以上为优秀．甲.乙.丙三人的各项成绩如下表.学期总评成绩优秀的是( )纸笔测试实践能力成长记录甲908395乙889095丙908890A. 甲 B. 乙.丙 C. 甲.乙 D. 甲.丙题目和参考答案——青夏教育精英家教网—

【题目】某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%，20%，30%的比例计入学期总评成绩，90分以上为优秀．甲、乙、丙三人的各项成绩如下表（单位：分），学期总评成绩优秀的是（）

	纸笔测试	实践能力	成长记录
甲	90	83	95
乙	88	90	95
丙	90	88	90

A. 甲 B. 乙、丙 C. 甲、乙 D. 甲、丙

【答案】C

【解析】由题意知，甲的总评成绩=90×50%+83×20%+95×30%=90.1，

乙的总评成绩=88×50%+90×20%+95×30%=90.5，

丙的总评成绩=90×50%+88×20%+90×30%=89.6，

∴甲、乙的学期总评成绩是优秀．

故选C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】一个不透明袋子中有1个红球，1个绿球和n个白球，这些球除颜色外无其他差别．

（1）当n=1时，从袋中随机摸出1个球，摸到红球和摸到白球的可能性是否相同？

（2）从袋中随机摸出一个球，记录其颜色，然后放回，大量重复该实验，发现摸到绿球的频率稳定于0.25，则n的值是；

（3）当n=2时，先从袋中任意摸出1个球不放回，再从袋中任意摸出1个球，请用列表或画树状图的方法，求两次都摸到白球的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）2 ，也可表示为c3+4（ab），即（a+b）2=c2+4（ab）由此推导出一个重要的结论a2+b2=c2 ，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．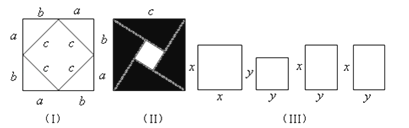

（1）请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．
（2）请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）2=x2+4xy+4y2 ．