
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回,大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是 ;
(3)当n=2时,先从袋中任意摸出1个球不放回,再从袋中任意摸出1个球,请用列表或画树状图的方法,求两次都摸到白球的概率.
【答案】(1)摸到红球和摸到白球的可能性相同;
(2)2;
(3)
两次摸出的球颜色不同的概率=![]() =
=![]() .
.
【解析】
试题分析:(1)当n=1时,利用概率公式可得到摸到红球和摸到白球的概率都为![]() ;
;
(2)利用频率估计概率,则摸到绿球的概率为0.25,根据概率公式得到![]() =0.25,然后解方程即可;
=0.25,然后解方程即可;
(3)先画树状图展示所有12种等可能的结果数,再找出两次摸出的球颜色不同的结果数,然后根据概率公式求解.
试题解析:(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性相同;
(2)利用频率估计概率得到摸到绿球的概率为0.25,
则![]() =0.25,解得n=2,
=0.25,解得n=2,
故答案为2;
(3)解:画树状图为:

共有12种等可能的结果数,其中两次摸出的球都是的结白色的结果共有2 种,
所以两次摸出的球颜色不同的概率=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在5×6的方格图中
在图1中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分)
在图2中,将线段A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分)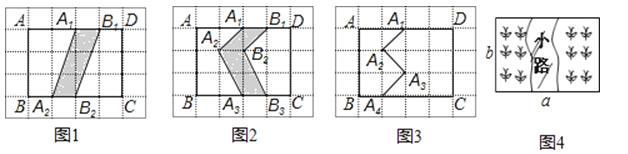
(1)在图3中,画出将折线A1A2A3A4向右平移1单位后的图形,并用阴影画出由这两条折线所围成的封闭图形.
(2)设上述三个图形中,矩形ABCD分别除去阴影部分后剩余部分的面积记为S1、S2、S3 , 则S1= ,S2= S3=
(3)如图4,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想草地部分的面积是 .(用含a、b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
(1)动手操作:
①如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD=
②如图2,若直角三角板ABC不动,改变等腰直角三角板DEF的位置,使三角板DEF的两条直角边DE、DF仍然分别经过点B、C,那么∠ABD+∠ACD= 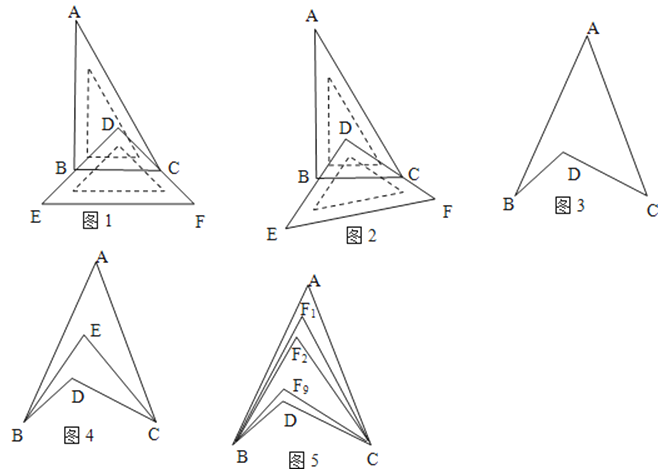
(2)猜想证明:
如图3,∠BDC与∠A、∠B、∠C之间存在着 关系
(3)灵活应用:
请你直接利用以上结论,解决以下列问题:
①如图4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,∠BEC
②如图5,∠ABD,∠ACD的10等分线相交于点F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,则∠A的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.减去一个数等于加上这个数
B.两个相反数相减得0
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛实验中,甲、乙两根蜡烛燃烧时剩余部分的高度![]() (cm)与燃烧时间
(cm)与燃烧时间![]() (h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:
(h)的关系如图所示. 请根据图像所提供的信息解答下列各问题:

(1)甲乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 ;
(2)分别求出甲、乙两根蜡烛燃烧时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
为何值时,甲、乙两根蜡烛在燃烧的过程中的高度相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
A. 甲 B. 乙、丙 C. 甲、乙 D. 甲、丙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com