
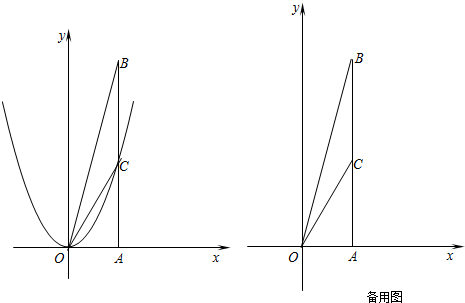
分析 (1)利用待定系数法即可解决问题.
(2)存在.设新抛物线C2与的顶点坐标为(m,2m),则N(m+2,2m+4),新抛物线C2的解析式为y=(x-m)2+2m,设点G的坐标为(x,y).分三种情形讨论①当BM为平行四边形MNBG的对角线时,则有$\frac{2+m}{2}$=$\frac{x+m+2}{2}$,$\frac{2m+8}{2}$=$\frac{y+2m+4}{2}$,推出x=0,y=4,推出点G坐标为(0,4),把(0,4)代入y=(x-m)2+2m,求出m即可.
②当BN为对角线时,方法类似.③当MN为对角线时,显然不成立.
解答 解:(1)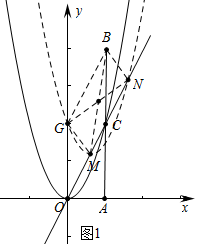 由题意C(2,4),设直线OC的解析式为y=kx,则有4=2k,
由题意C(2,4),设直线OC的解析式为y=kx,则有4=2k,
∴k=2,
∴直线OC的解析式为y=2x,
设以原点O为顶点的抛物线C1的解析式为y=ax2,把C(2,4)代入得a=1,
∴以原点O为顶点的抛物线C1的解析式为y=x2,
故答案为y=2x,y=x2.
(2)存在.理由如下,
设新抛物线C2与的顶点坐标为(m,2m),则N(m+2,2m+4),新抛物线C2的解析式为y=(x-m)2+2m.
设点G的坐标为(x,y).
①当BM为平行四边形MNBG的对角线时,则有$\frac{2+m}{2}$=$\frac{x+m+2}{2}$,$\frac{2m+8}{2}$=$\frac{y+2m+4}{2}$,
∴x=0,y=4,
∴点G坐标为(0,4),把(0,4)代入y=(x-m)2+2m,得到m=-1+$\sqrt{5}$或-1-$\sqrt{5}$,
此时抛物线C2的解析式为y=(x+1-$\sqrt{5}$)2-2+2$\sqrt{5}$或y=(x+1+$\sqrt{5}$)2-2-2$\sqrt{5}$.
②当BN为对角线时,则有$\frac{2+m+2}{2}$=$\frac{x+m}{2}$,$\frac{8+2m+4}{2}$=$\frac{2m+y}{2}$,
∴x=4,y=12,
∴点G的坐标为(4,12),把(4,12)代入y=(x-m)2+2m,得到m=3-$\sqrt{5}$或3+$\sqrt{5}$
∴此时抛物线C2的解析式为y=(x-3+$\sqrt{5}$)2+6-2$\sqrt{5}$或y=(x-3-$\sqrt{5}$)2+6+2$\sqrt{5}$.
③当MN为对角线时,显然不成立.
综上所述,满足条件的抛物线C2的解析式为y=(x+1-$\sqrt{5}$)2-2+2$\sqrt{5}$或y=(x+1+$\sqrt{5}$)2-2-2$\sqrt{5}$或y=(x-3+$\sqrt{5}$)2+6-2$\sqrt{5}$或y=(x-3-$\sqrt{5}$)2+6+2$\sqrt{5}$.
点评 本题主要考查了二次函数综合题、一次函数的应用、平行四边形的性质和判定、中点坐标公式等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
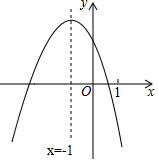 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1207×1011 | B. | 1.207×1010 | C. | 1.207×1011 | D. | 1207×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com