
【题目】如图,Rt△ABC的边BC位于直线l上,AC=![]() ,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).
,∠ACB=90o,∠A=30o,若△RtABC由现在的位置向右无滑动地翻转,当点A第3次落在直线上l时,点A所经过的路线的长为________________(结果用含л的式子表示).

科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD,点 E,F 分别在 AD,CD 上,且DE=CF,AF 与 BE 相交于点G.
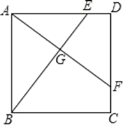
(1)求证:AF⊥BE;
(2)若 AB=6,DE=2,AG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )

A. 60° B. 90° C. 30° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C,已知抛物线的对称轴为x=1,B(3,0),C(0,-3),
(1)求二次函数y=ax2+bx+c的解析式;
(2)在抛物线对称轴上是否存在一点P,使点P到B、C两点距离之差最大?若存在,求出P点坐标;若不存在,请说明理由;
(3)平行于x轴的一条直线交抛物线于M,N两点,若以MN为直径的圆恰好与x轴相切,求此圆的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某体育用品商店,购买50根跳绳和80个毽子共用1120元,购买30根跳绳和50个毽子共用680元.
(1)跳绳、毽子的单价各是多少元?
(2)该店在“元旦”节期间开展促销活动,所有商品按同样的折数打折销售.节日期间购买100根跳绳和100个毽子只需1700元,该店的商品按原价的几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.

【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: ![]() 根据同角的余角相等可得到
根据同角的余角相等可得到![]() 结合条件
结合条件![]() ,再加上
,再加上![]() 可证得结论;
可证得结论;![]() 根据
根据![]() 得到
得到![]() 根据等腰三角形的性质得到
根据等腰三角形的性质得到![]() 由平角的定义得到
由平角的定义得到![]()
试题解析: ![]() 证明:
证明:

![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是∠AOB的平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D.下列结论 不一定成立的是( )

A.∠AOP=∠BOPB.PC=PD
C.∠OPC=∠OPDD.OP=PC+PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个n位自然数![]() 能被x0整除,依次轮换个位数字得到的新数
能被x0整除,依次轮换个位数字得到的新数![]() 能被x0+1整除,再依次轮换个位数字得到的新数
能被x0+1整除,再依次轮换个位数字得到的新数![]() 能被x0+2整除,按此规律轮换后,
能被x0+2整除,按此规律轮换后,![]() 能被x0+3整除,…,
能被x0+3整除,…,![]() 能被x0+n﹣1整除,则称这个n位数
能被x0+n﹣1整除,则称这个n位数![]() 是x0的一个“轮换数”.
是x0的一个“轮换数”.
例如:60能被5整除,06能被6整除,则称两位数60是5的一个“轮换数”;
再如:324能被2整除,243能被3整除,432能被4整除,则称三位数324是2个一个“轮换数”.
(1)若一个两位自然数的个位数字是十位数字的2倍,求证这个两位自然数一定是“轮换数”.
(2)若三位自然数![]() 是3的一个“轮换数”,其中a=2,求这个三位自然数
是3的一个“轮换数”,其中a=2,求这个三位自然数![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com