
【题目】已知x1 , x2是方程x2﹣(k﹣2)x+k2+3k+5=0的实数根(x1 , x2可相等)
(1)证明方程的两根都小于0;
(2)当实数k取何值时x12+x22最大?并求出最大值.
【答案】(1)证明:∵△=(k﹣2)2﹣4(k2+3k+5)≥0,
∴﹣4≤k≤﹣![]() ,
,
∵x1+x2=k﹣2,x1x2=k2+3k+5,
∴x1+x2=k﹣2<0,x1x2=k2+3k+5>0,
∴方程的两根都小于0;
(2)解:x12+x22=(x1+x2)2﹣2x1x2=(k﹣2)2﹣2(k2+3k+5)=﹣k2﹣10k﹣6=﹣(k+5)2+19,
∵﹣4≤k≤﹣![]() ,
,
∴k=﹣4时,x12+x22有最大值,最大值为﹣(﹣4+5)2+19=18.
【解析】(1)根据判别式的意义得到△=(k﹣2)2﹣4(k2+3k+5)≥0,解此不等式得到﹣4≤k≤﹣![]() , 再由根与系数的关系得x1+x2=k﹣2,x1x2=k2+3k+5,利用k的取值范围有x1+x2=k﹣2<0,x1x2=k2+3k+5>0,于是利用有理数的性质即可判断方程的两根都小于0;
, 再由根与系数的关系得x1+x2=k﹣2,x1x2=k2+3k+5,利用k的取值范围有x1+x2=k﹣2<0,x1x2=k2+3k+5>0,于是利用有理数的性质即可判断方程的两根都小于0;
(2)利用完全平方公式得到x12+x22=(x1+x2)2﹣2x1x2=(k﹣2)2﹣2(k2+3k+5)=﹣(k+5)2+19,然后根据二次函数的最值问题求解.
【考点精析】本题主要考查了求根公式和根与系数的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商才能正确解答此题.


科目:初中数学 来源: 题型:
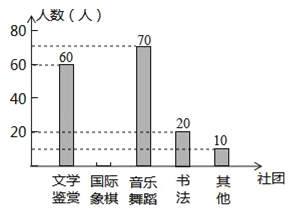
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):

根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1). 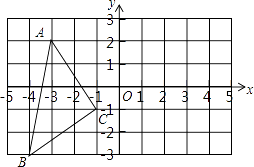
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1 , B1 , C1的坐标(直接写答案):A1;B1;C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com