
【题目】我们给出如下定义,如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形,那么这个四边形叫做等垂四边形,这条对角线叫做这个四边形的等垂对角线.
(1)已知![]() 是四边形
是四边形![]() 的等垂对角线,
的等垂对角线,![]() ,
,![]() 均为钝角,且
均为钝角,且![]() 比
比![]() 大
大![]() ,那么
,那么![]() ________.
________.
(2)如图,已知![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,![]() 、
、![]() 两点分别在
两点分别在![]() 、
、![]() 边上,
边上,![]() ,
,![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是等垂四边形。
是等垂四边形。

【答案】(1)110°或150°;(2)见解析.
【解析】
(1)由题意分∠D=90°与∠DCA=90°两种情况,并利用四边形内角和定理求解即可;
(2)连接![]() ,先利用SAS证明
,先利用SAS证明![]() ,再证明
,再证明![]() 是等边三角形,最后利用勾股定理的逆定理证明
是等边三角形,最后利用勾股定理的逆定理证明![]() 是直角三角形即可.
是直角三角形即可.
解:(1)![]() 或
或![]() .
.
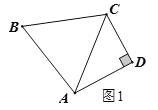
如图1,当∠D=90°时,设![]() =x°,则
=x°,则![]() =(x-10)°,根据四边形内角和定理可得:
=(x-10)°,根据四边形内角和定理可得:
x+x-10+90+60=360,解得x=110,即![]() 110°;
110°;
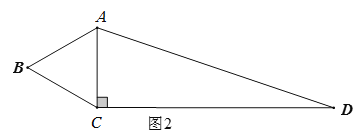
如图2,当∠DCA=90°时,![]() 60°+90°=150°;
60°+90°=150°;
故答案为![]() 或
或![]() .
.
(2)证明:如图3,连接![]() .
.
∵![]() 和
和![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∴四边形![]() 是等垂四边形.
是等垂四边形.



科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中![]() ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2![]() m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为![]() ;设包装盒底面的长为
;设包装盒底面的长为![]() .
.
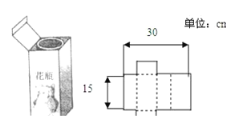
(1)用![]() 表示包装盒底面的宽;
表示包装盒底面的宽;
(2)用![]() 表示包装盒的表面积,并化简;
表示包装盒的表面积,并化简;
(3)若包装盒底面的长为![]() ,求包装盒的表面积.
,求包装盒的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
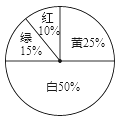
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(如下图),并规定:购买100元的商品,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、绿、黄、白区域,那么顾客就可以分别得到80元、30元、10元、0元的购物券,凭购物券仍然可以在商场购物;如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)每转动一次转盘所获购物券金额的平均数是多少?
(2)若在此商场购买100元的货物,那么你将选择哪种方式获得购物券?
(3)小明在家里也做了一个同样的转盘做实验,转10次后共获得购物券96元,他说还是不转转盘直接领取购物券合算,你同意小明的说法吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com