
【题目】完成下面推理过程: 如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE=()
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ![]() ()
()
∠ABE= ![]() ()
()
∴∠ADF=∠ABE
∴∥()
∴∠FDE=∠DEB.()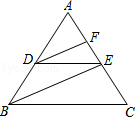
【答案】∠ABC;两直线平行,同位角相等;∠ADE;角平分线定义;∠ABC;角平分线定义;DF;BE;同位角相等,两直线平行;两直线平行,内错角相等
【解析】解:理由是:∵DE∥BC(已知), ∴∠ADE=∠ABC(两直线平行,同位角相等),
∵DF、BE分别平分ADE、∠ABC,
∴∠ADF= ![]() ∠ADE(角平分线定义),
∠ADE(角平分线定义),
∠ABE= ![]() ∠ABC(角平分线定义),
∠ABC(角平分线定义),
∴∠ADF=∠ABE,
∴DF∥BE(同位角相等,两直线平行),
∴∠FDE=∠DEB(两直线平行,内错角相等),
所以答案是:∠ABC,两直线平行,同位角相等;∠ADE,角平分线定义;∠ABC,角平分线定义;DF,BE,同位角相等,两直线平行;两直线平行,内错角相等.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
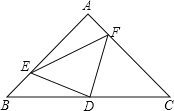
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路边建一个物流站(C点),使之与该公司A及车站D的距离相等,求物流站与车站之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是( ) 
A.150°
B.180°
C.270°
D.360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).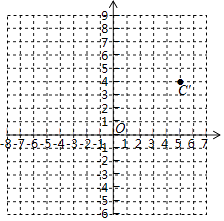
(1)画出△ABC,并求△ABC的面积;在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′,画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(2)P(﹣3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,﹣3),则m= , n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com