
初中生对待学习的态度一直是教育工作者关注的问题之一.为此无锡市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;
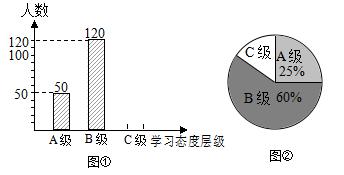
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
科目:初中数学 来源: 题型:
如图,已知反比例函数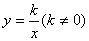 的图象经过点(
的图象经过点(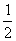 ,8),直线
,8),直线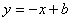 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4,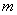 ).
).

(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 轴、
轴、 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
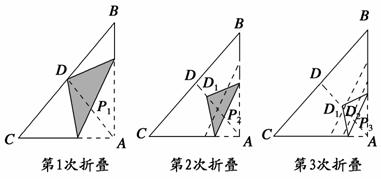
如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )
A.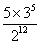 B.
B. C.
C.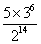 D.
D.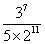
查看答案和解析>>
科目:初中数学 来源: 题型:
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
|


(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线 过点
过点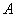 (,
(,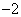 ),
),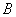 (3,
(3,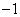 ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
对于实数x,我们规定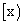 表示大于
表示大于 x的
x的 最小整数,如
最小整数,如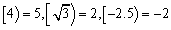 ,现对64进行如下操作:
,现对64进行如下操作: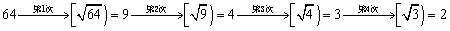 ,这样对64只需进行4次操作后变为2,类似地,
,这样对64只需进行4次操作后变为2,类似地, 只需进行4次操作后变为2的所有正整数中,
只需进行4次操作后变为2的所有正整数中, 最大的是 .
最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解: 对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果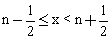 ,则<x>=n。
,则<x>=n。
如:<0>=<0.49>=0,<0.64>=<1.393>=1,<3>=3,<2.5>=<3.12>=3,…
试解决下列问题:
(1)填空:如果<3x-2>=4,则实数x的取值范围为 ;
(2)当
 ,m为非负整数时,
,m为非负整数时, 求证:
求证: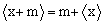 ;
;
(3)求满足 的所有非负实数x的值;
的所有非负实数x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
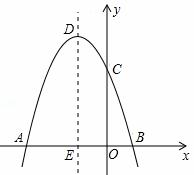
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0, 3)。
(1)求抛物线的解析式;
(2)若点P为抛物 线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com