
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
|


(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
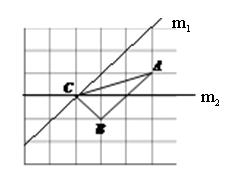
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线 过点
过点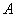 (,
(,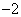 ),
),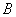 (3,
(3,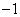 ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
(1)见解析;(2)图形详见解析;(3)存在点P(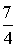 ,-
,-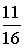 ) 或(-2,-
) 或(-2,-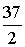 )使S△APC=S△BPC.
)使S△APC=S△BPC.
【解析】(1)分别作AE⊥CD,BF⊥CD,垂足为E,F
∴∠AEP=∠BFP=90°∵P是AB中点, ∴AP=BP又∵∠APE=∠BPF∴△AEP≌△AFP
∴AE=BF,即直线CD是点A、B的一条等距线.

(2)如图,直线m1、m2就是所有的直线
(3)由题意知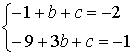 ,得
,得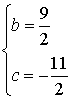 ,∴抛物线为y=-x2+
,∴抛物线为y=-x2+ x-
x-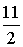
∵S△ APC=S△BPC.,∴A、B两点到直线PC的距离相等
APC=S△BPC.,∴A、B两点到直线PC的距离相等
①当PC∥AB时,计算得直线AB解析式为y= x-
x- ,直线CP解析式为y=
,直线CP解析式为y= x-
x-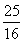
解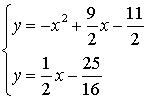 ,得x1=
,得x1=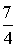 ,x2=
,x2= ;∴点P(
;∴点P(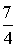 ,-
,-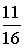 );
);
②当直线CP过AB中点时,易求AB中点E(2,-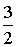 ),直线CE解析式为y=
),直线CE解析式为y=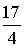 x-1
x-1 0,
0,
解 ,得x1=2,x2=
,得x1=2,x2= ;;∴点P(-2,-
;;∴点P(-2,-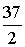 )
)
综上所述存在点P(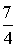 ,-
,-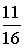 ) 或(-2,-
) 或(-2,-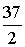 ) 使S△APC=S△BPC.
) 使S△APC=S△BPC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(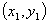 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为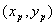 .由
.由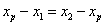 ,得
,得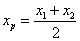 ,同理
,同理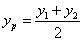 ,所以AB的中点坐标为(
,所以AB的中点坐标为(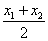 ,
, ).由勾股定理得
).由勾股定理得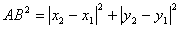 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=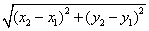 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l: 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.


(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
初中生对待学习的态度一直是教育工作者关注的问题之一.为此无锡市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;
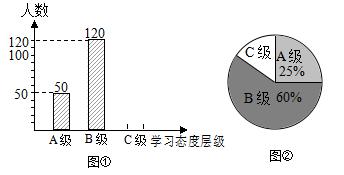
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
定义一种新运算:观察下列各式:
1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4=5×4+4=24 ;4⊙(-3)= 4×4-3=13
(1)请你想一想:a⊙b=___________;
(2)若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ;
(3)若a⊙(-2b) = 4,请计算 (a-b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
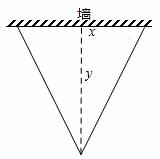
如图,某小区要围成一个等腰三角 形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24
形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24 平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
 A.
A. 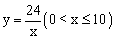 B.
B. 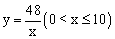
 C.
C. 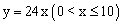 D.
D. 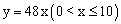
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com