
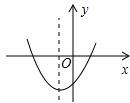
二次函数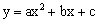 的图象如图所示,反比例函数
的图象如图所示,反比例函数 与一次函数
与一次函数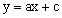 在同一平面直角坐标系中的大致图象是【 】
在同一平面直角坐标系中的大致图象是【 】
A. B.
B.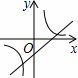

 C.
C. D.
D.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如果有两点到一条直线的距离相等,那么称这条直线为 “两点的等距线”.
|


(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线 过点
过点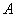 (,
(,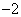 ),
),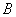 (3,
(3,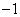 ),顶点为C.抛物线上是否存在点P ,使
),顶点为C.抛物线上是否存在点P ,使 ,若存在,求出点P的坐标;若不存在,请说明理由。
,若存在,求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数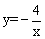 的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
A.y3 <y1<y2 B.y1<y
<y1<y2 B.y1<y
 2<y3 C.y3<y2<y1 D.y2<y3<y1
2<y3 C.y3<y2<y1 D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
市政府为改善居民的居住环境,修建了环境幽雅的环城公园,为了给公园内的草评定期喷水,安装了一些自动旋转喷水器,如图所示,设喷水管
 高出地面1.5m,在
高出地面1.5m,在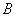
 处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头
处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头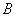
 与水流最高点
与水流最高点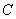
 的连线与地平面成
的连线与地平面成
 的角,水流的最高点
的角,水流的最高点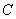
 离地平面距离比喷水头
离地平面距离比喷水头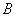
 离地平面距离高出2m,水流的落地点为
离地平面距离高出2m,水流的落地点为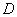
 .在建立如图所示的直角坐标系中:
.在建立如图所示的直角坐标系中:
(1)求抛物线的函数解析式;
(2)求水流的落地点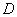
 到
到
 点的距离是多少m?
点的距离是多少m?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0, 3)。
(1)求抛物线的解析式;
(2)若点P为抛物 线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知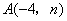
 ,
,
 是一
是一 次函数
次函数
 的图象和反比例函数
的图象和反比例函数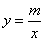

 的图象的两个交点.
的图象的两个交点.
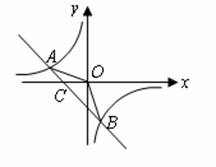

(1)求反比例函数和一次函数的函数关系式;
(2)求△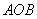
 的面积;
的面积;
(3)则方程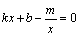
 的解是
的解是  ;(请直接写出答案)
;(请直接写出答案)
(4)则不等式
 的解集是 .(请直接写出答案)
的解集是 .(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
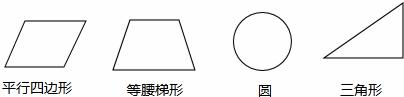
四张质地、大小相同的卡片上,分别画上如下图所示的四个图形, 在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是
在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是 中心对称图形的概率为【 】
中心对称图形的概率为【 】
A. 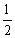 B.
B. 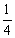
 C.
C. 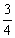 D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=3,BC=4,E、F分别是边CD、AD上的点,且CE=1,AF= ,
, AE、BF相交于点O,下列结论:(1)BF =
AE、BF相交于点O,下列结论:(1)BF =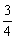 AE;(2)AE⊥BF;(3)
AE;(2)AE⊥BF;(3)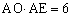 ;(4)
;(4) 中正确的
中正确的 有【 】
有【 】

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
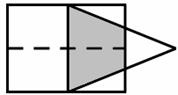
如图,矩形的长 和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形
和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形 自左向右运动的距离为x,那么y关于x的函数关系式为
自左向右运动的距离为x,那么y关于x的函数关系式为
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com