
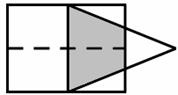
如图,矩形的长 和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形
和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形 自左向右运动的距离为x,那么y关于x的函数关系式为
自左向右运动的距离为x,那么y关于x的函数关系式为
。
科目:初中数学 来源: 题型:
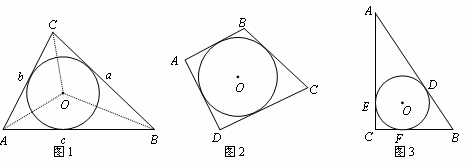
【阅读材料】己知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切⊙O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△ OAC+S△OAB=
OAC+S△OAB=
 BC·r+
BC·r+
 AC·r+
AC·r+
 AB·r=
AB·r=
 a·r+
a·r+
 b·r+
b·r+
 c·r=
c·r=
 (a+b+c)r
(a+b+c)r
∴

(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分 别为AB=a,
别为AB=a, BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理 解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.
解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知⊙O的直径CD为4,弧AC的度数为120°,弧BC的度数为30°,在直径CD上作出点P,使BP+AP的值最小,若BP+AP的值最小,则BP+AP的最小值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
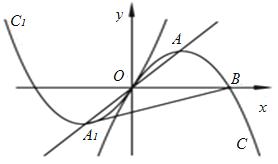
已知抛物线C: 过原点,与
过原点,与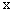 轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为
轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为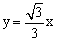 ,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。
,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,长是2宽是1的矩形和边长是1的正三角形,矩形的一长边与正三角形的一边在同一水平线上,三角形沿 该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】
该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】

A.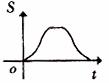 B.
B.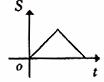 C.
C.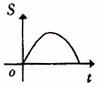 D.
D.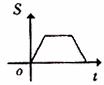
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系式.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com