
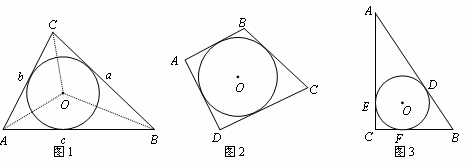
【阅读材料】己知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切⊙O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△ OAC+S△OAB=
OAC+S△OAB=
 BC·r+
BC·r+
 AC·r+
AC·r+
 AB·r=
AB·r=
 a·r+
a·r+
 b·r+
b·r+
 c·r=
c·r=
 (a+b+c)r
(a+b+c)r
∴

(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分 别为AB=a,
别为AB=a, BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理 解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.
解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数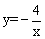 的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
A.y3 <y1<y2 B.y1<y
<y1<y2 B.y1<y
 2<y3 C.y3<y2<y1 D.y2<y3<y1
2<y3 C.y3<y2<y1 D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
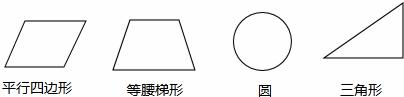
四张质地、大小相同的卡片上,分别画上如下图所示的四个图形, 在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是
在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是 中心对称图形的概率为【 】
中心对称图形的概率为【 】
A. 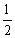 B.
B. 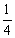
 C.
C. 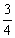 D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=3,BC=4,E、F分别是边CD、AD上的点,且CE=1,AF= ,
, AE、BF相交于点O,下列结论:(1)BF =
AE、BF相交于点O,下列结论:(1)BF =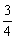 AE;(2)AE⊥BF;(3)
AE;(2)AE⊥BF;(3)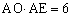 ;(4)
;(4) 中正确的
中正确的 有【 】
有【 】

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=1,AB= ,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。
,在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°,当点E是AB的中点时,线段DF的长度是 。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()
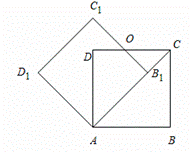

A.
 B.
B.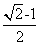
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
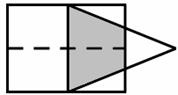
如图,矩形的长 和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形
和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形 自左向右运动的距离为x,那么y关于x的函数关系式为
自左向右运动的距离为x,那么y关于x的函数关系式为
。
查看答案和解析>>
科目:初中数学 来源: 题型:
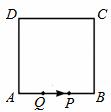
如图,在边长为4的正方形ABCD中,动点P,Q同时从A点出发,沿AB →BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q
→BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q 两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com