
如图,矩形ABCD中,AB=3,BC=4,E、F分别是边CD、AD上的点,且CE=1,AF= ,
, AE、BF相交于点O,下列结论:(1)BF =
AE、BF相交于点O,下列结论:(1)BF =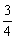 AE;(2)AE⊥BF;(3)
AE;(2)AE⊥BF;(3)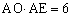 ;(4)
;(4) 中正确的
中正确的 有【 】
有【 】

A. 4个 B. 3个 C. 2个 D. 1个
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
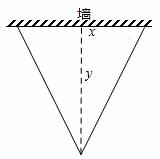
如图,某小区要围成一个等腰三角 形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24
形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24 平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
 A.
A. 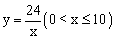 B.
B. 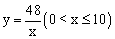
 C.
C. 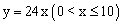 D.
D. 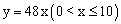
查看答案和解析>>
科目:初中数学 来源: 题型:
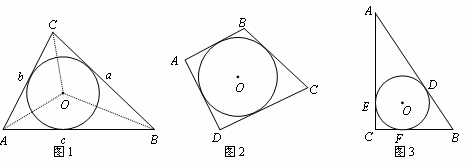
【阅读材料】己知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切⊙O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△ OAC+S△OAB=
OAC+S△OAB=
 BC·r+
BC·r+
 AC·r+
AC·r+
 AB·r=
AB·r=
 a·r+
a·r+
 b·r+
b·r+
 c·r=
c·r=
 (a+b+c)r
(a+b+c)r
∴

(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分 别为AB=a,
别为AB=a, BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理 解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.
解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知⊙O的直径CD为4,弧AC的度数为120°,弧BC的度数为30°,在直径CD上作出点P,使BP+AP的值最小,若BP+AP的值最小,则BP+AP的最小值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,长是2宽是1的矩形和边长是1的正三角形,矩形的一长边与正三角形的一边在同一水平线上,三角形沿 该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】
该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】

A.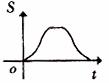 B.
B.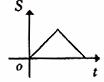 C.
C.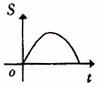 D.
D.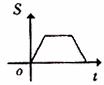
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com