
点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数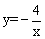 的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
A.y3 <y1<y2 B.y1<y
<y1<y2 B.y1<y
 2<y3 C.y3<y2<y1 D.y2<y3<y1
2<y3 C.y3<y2<y1 D.y2<y3<y1
科目:初中数学 来源: 题型:
阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(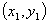 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为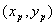 .由
.由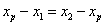 ,得
,得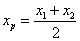 ,同理
,同理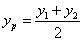 ,所以AB的中点坐标为(
,所以AB的中点坐标为(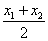 ,
, ).由勾股定理得
).由勾股定理得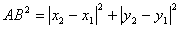 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=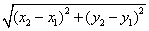 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l: 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.


(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义一种新运算:观察下列各式:
1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4=5×4+4=24 ;4⊙(-3)= 4×4-3=13
(1)请你想一想:a⊙b=___________;
(2)若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ;
(3)若a⊙(-2b) = 4,请计算 (a-b)⊙(2a+b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某小区要围成一个等腰三角 形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24
形花圃,花圃的等腰三角形底边利用足够长的墙,墙的长度为10米,围成的花圃面积恰好为24 平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
平方米。设等腰三角形底边的长为x米,底边上的高为y米,则y与x之间的函数关系式是【 】.
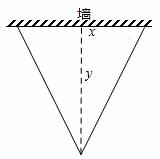
 A.
A. 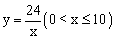 B.
B. 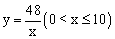
 C.
C. 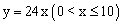 D.
D. 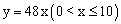
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两车从A地驶 向B地,
向B地, 甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
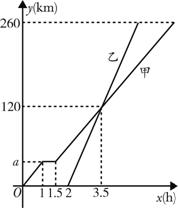

(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函
 数表达式
数表达式 ,并写出相应
,并写出相应 的x的取值范围;
的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
查看答案和解析>>
科目:初中数学 来源: 题型:
B。
【考点】一次函数和反比例函数的性质,曲线上点的坐标与方程的关系,不等式的性质,排它法的应用。
【分析】∵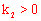 ,∴双曲线
,∴双曲线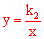 的图象在一、三象限。故排除C。
的图象在一、三象限。故排除C。
又∵函数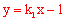 的
的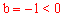 ,
,
∴直线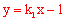 与
与 轴的交点在
轴的交点在 轴下
轴下 方。故排除D。
方。故排除D。
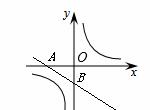
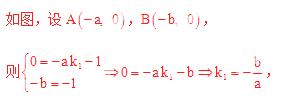
 又∵
又∵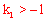 ,
, ∴
∴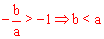 ,即OB<OA。故排除A。
,即OB<OA。故排除A。
查看答案和解析>>
科目:初中数学 来源: 题型:
已知 抛
抛 物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
A.第四象限 B.第三象限 C.第二象限 D.第一象限
查看答案和解析>>
科目:初中数学 来源: 题型:
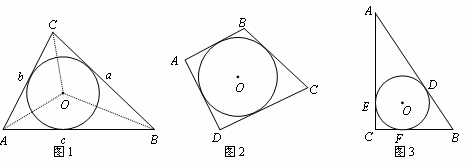
【阅读材料】己知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切⊙O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△ OAC+S△OAB=
OAC+S△OAB=
 BC·r+
BC·r+
 AC·r+
AC·r+
 AB·r=
AB·r=
 a·r+
a·r+
 b·r+
b·r+
 c·r=
c·r=
 (a+b+c)r
(a+b+c)r
∴

(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分 别为AB=a,
别为AB=a, BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理 解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.
解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com