
已知 抛
抛 物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
物线y=ax2﹣2x+c与y轴交于x轴上方,与x轴没有交点,那么该抛物线的顶点所在的象限是【 】
A.第四象限 B.第三象限 C.第二象限 D.第一象限
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
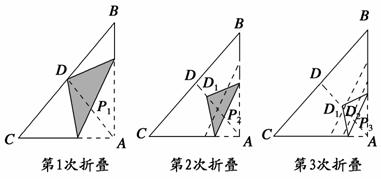
如图,直角三角形纸片ABC中,AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交与点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于点P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;…;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )
A.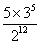 B.
B. C.
C.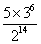 D.
D.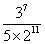
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解: 对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果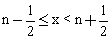 ,则<x>=n。
,则<x>=n。
如:<0>=<0.49>=0,<0.64>=<1.393>=1,<3>=3,<2.5>=<3.12>=3,…
试解决下列问题:
(1)填空:如果<3x-2>=4,则实数x的取值范围为 ;
(2)当
 ,m为非负整数时,
,m为非负整数时, 求证:
求证: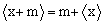 ;
;
(3)求满足 的所有非负实数x的值;
的所有非负实数x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数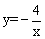 的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是【 】
A.y3 <y1<y2 B.y1<y
<y1<y2 B.y1<y
 2<y3 C.y3<y2<y1 D.y2<y3<y1
2<y3 C.y3<y2<y1 D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
市政府为改善居民的居住环境,修建了环境幽雅的环城公园,为了给公园内的草评定期喷水,安装了一些自动旋转喷水器,如图所示,设喷水管
 高出地面1.5m,在
高出地面1.5m,在
 处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头
处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头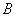
 与水流最高点
与水流最高点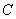
 的连线与地平面成
的连线与地平面成
 的角,水流的最高点
的角,水流的最高点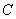
 离地平面距离比喷水头
离地平面距离比喷水头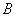
 离地平面距离高出2m,水流的落地点为
离地平面距离高出2m,水流的落地点为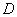
 .在建立如图所示的直角坐标系中:
.在建立如图所示的直角坐标系中:
(1)求抛物线的函数解析式;
(2)求水流的落地点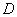
 到
到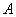
 点的距离是多少m?
点的距离是多少m?
查看答案和解析>>
科目:初中数学 来源: 题型:
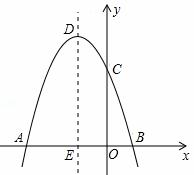
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0, 3)。
(1)求抛物线的解析式;
(2)若点P为抛物 线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
线在第二象限上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是等腰直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
四张质地、大小相同的卡片上,分别画上如下图所示的四个图形, 在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是
在看不到图形的情况下从中任意抽出一张,则抽出的卡片既不是轴对称图形也不是 中心对称图形的概率为【 】
中心对称图形的概率为【 】
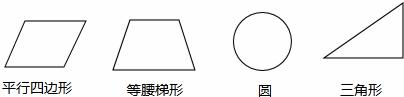
A. 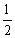 B.
B. 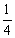
 C.
C. 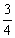 D.1
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com