
如图,已知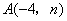
 ,
,
 是一
是一 次函数
次函数
 的图象和反比例函数
的图象和反比例函数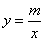

 的图象的两个交点.
的图象的两个交点.
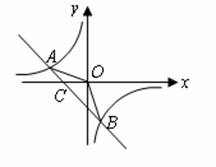

(1)求反比例函数和一次函数的函数关系式;
(2)求△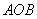
 的面积;
的面积;
(3)则方程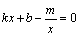
 的解是
的解是  ;(请直接写出答案)
;(请直接写出答案)
(4)则不等式
 的解集是 .(请直接写出答案)
的解集是 .(请直接写出答案)
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
B。
【考点】一次函数和反比例函数的性质,曲线上点的坐标与方程的关系,不等式的性质,排它法的应用。
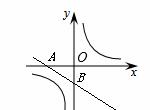
【分析】∵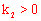 ,∴双曲线
,∴双曲线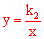 的图象在一、三象限。故排除C。
的图象在一、三象限。故排除C。
又∵函数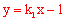 的
的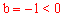 ,
,
∴直线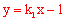 与
与 轴的交点在
轴的交点在 轴下
轴下 方。故排除D。
方。故排除D。
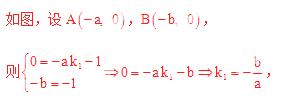
 又∵
又∵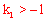 ,
, ∴
∴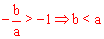 ,即OB<OA。故排除A。
,即OB<OA。故排除A。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A是抛物线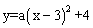 与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为斜边的等腰直角三角形ABC的顶点C的坐标为 .
与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为斜边的等腰直角三角形ABC的顶点C的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
某商家经销一种商品,用于装修门面已投资3000元。已知该商品每千克成本50元,在第一个月的试销时间内发现项,当销售单价为70元/ kg时,销售量为100 kg,销量w(kg)随销售单价x(元/ kg)的变化而变化,销售单价每提高5元/ kg,销售量减少10 kg。
设该商品的月销售利润为y(元)(销售利润=单价× 销售量-成本-投资)。
销售量-成本-投资)。
(1)请根据上表,写出w与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求y与x之间的函数关系 式(不必写出自变量x的取值范围),并求出x为何值时,y的
式(不必写出自变量x的取值范围),并求出x为何值时,y的 值最大?
值最大?
(3)若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700,那么第二 个月时里应该确定销售
个月时里应该确定销售 单价为多少元?
单价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com