
如图,已知反比例函数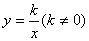 的图象经过点(
的图象经过点(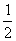 ,8),直线
,8),直线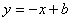 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4,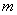 ).
).

(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与 轴、
轴、 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线,交BC于点E.
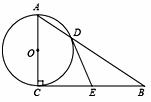
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 .
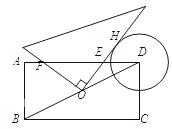
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读材料:如图1,在平面直角坐标系中,A.B两点的坐标分别为A(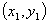 ,B
,B ,AB中点P的坐标为
,AB中点P的坐标为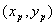 .由
.由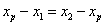 ,得
,得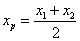 ,同理
,同理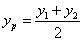 ,所以AB的中点坐标为(
,所以AB的中点坐标为(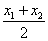 ,
, ).由勾股定理得
).由勾股定理得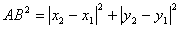 ,所以A、B两点间的距离公式为AB=
,所以A、B两点间的距离公式为AB=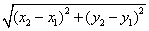 .
.
注:上述公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题:
如图2,直线l: 与抛物线
与抛物线 交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.


(1)求A、B两点的坐标及P、C两点的坐标;
(2)连结AB、AC,求证:△ABC为直角三角形;
(3)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
初中生对待学习的态度一直是教育工作者关注的问题之一.为此无锡市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
 (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;
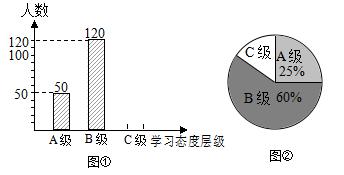
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两车从A地驶 向B地,
向B地, 甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
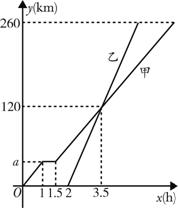

(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函
 数表达式
数表达式 ,并写出相应
,并写出相应 的x的取值范围;
的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com