练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D的切线，交BC于点E．

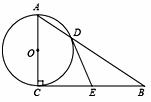
    （1）求证：EB=EC；

    （2）若以点O、D、E、C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．


    （1）证明见解析；（2）△ABC是等腰直角三角形，理由见解析

    【解析】（1）连接CD，∵AC是直径，∠ACB=90°，∴BC是⊙O的切线，∠CDA=90°．

    ∵DE是⊙O的切线，∴DE=CE   ∴∠DCE=∠CDE．又∵∠DCE+∠EBD=∠CDE+∠EDB=90°，

    ∴∠EBD=∠EDB，∴DE=CE，又∵DE=BE，∴CE=BE．

    （2）当以点O、D、E、C为顶点的四边形是正方形时，则∠DEB=90°，

    又∵DE=BE，∴△DEB是等腰直角三角形，则∠B=45°，∴△ABC是等腰直角三角形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，△ABC绕点A顺时针旋转45°得到△，若∠BAC=90°，AB=AC=，则图中阴影部分的面积等于         。 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


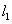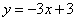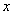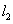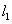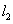    如图，直线的解析表达式为，且与轴交于点D，直线经过点A，B，直线和交于点C．

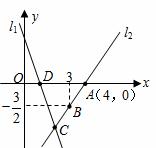
    （1）求直线的解析表达式；

    （2）求△ADC的面积；

    （3）直线上存在异于点C的另一点P，使△ADP与△ADC面积相等，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：=             ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，是用火柴棒拼成的图形，第1个图形需3根火柴棒，第2个图形需5根火柴棒，第3个图形需7根火柴棒，第4个图形需     根火柴棒，……，则第个图形需   根火柴棒。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


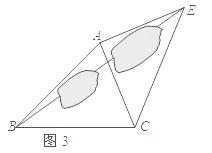
    1）如图1，已知△ABC，以AB，AC为边向△ABC外做等边△ABD和等边△ACE．连接BE，CD．请你完成图形，并证明：BE=CD；（尺规作图，不写做法，保留作图痕迹）

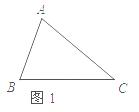
    （2）如图2，已知△ABC，以AB，AC为边向外做正方形ABFD和正方形ACGE．连接BE，CD．BE与CD有什么数量关系？简单说明理由．

    （3）运用（1）、（2）解答中所积累的经验和知识，完成下题：

    如图3，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC＝45°，∠CAE＝90°，AB＝BC＝10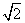米，AC＝AE．求BE的长．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


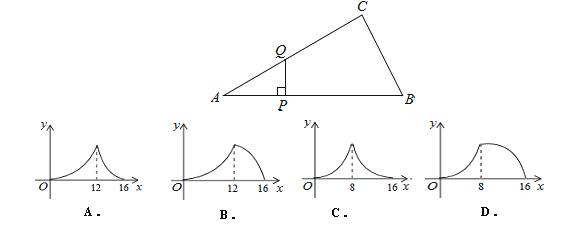
    如图，△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上一点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（  ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知反比例函数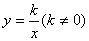的图象经过点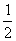（，8），直线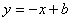经过该反比例函数图象上的点Q（4，）．

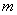    （1）求上述反比例函数和直线的函数表达式；

    （2）设该直线与轴、轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    对于实数x，我们规定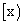表示大于x的最小整数，如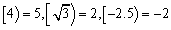，现对64进行如下操作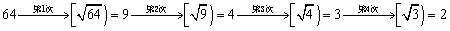：，这样对64只需进行4次操作后变为2，类似地，只需进行4次操作后变为2的所有正整数中，最大的是          .

    查看答案和解析>>

    同步练习册答案